




Next: Elastic energy and the
Up: Berryman: Seismic waves in
Previous: INTRODUCTION
Prior work on effective medium theory (Berryman, 1995) and double-porosity
dual-permeability modeling (Berryman and Wang, 2000; Berryman and
Pride, 2002a; Pride and Berryman, 2003a,b)
has most often involved calculation of
isotropic properties. In almost all cases, it is much harder to estimate
anisotropic properties because the first step in such a calculation
requires knowledge of both the effects of an oriented inclusion, and
knowledge of a distribution (both in space and in orientation)
of such inclusions. Then an additional calculation of the overall
properties based on microdistribution information is needed.
Unfortunately, we will seldom know the microdistribution of the
inclusions, and so we are immediately limited in what we can do
scientifically along these lines in most cases. However, there is one
exception to this that arises in the case of flat cracks in otherwise
elastic media. This problem was originally studied in some detail by
O'Connell and Budiansky (1976) and Budiansky and O'Connell (1977).
They showed in particular that, in the flat crack limit, a single
parameter -- the crack density 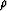 -- was sufficient to describe
the behavior of isotropic systems. This analysis was good for
representing the behavior at very low crack densities. In order to arrive at
higher crack densities, these authors made use of an older effective
medium theory sometimes called ``self-consistent'', and sometimes
more accurately described as ``asymmetric self-consistent.''
This approach had the drawback
that it overpredicted the effect of cracks on reducing elastic compliance,
and therefore gave a relatively low value
-- was sufficient to describe
the behavior of isotropic systems. This analysis was good for
representing the behavior at very low crack densities. In order to arrive at
higher crack densities, these authors made use of an older effective
medium theory sometimes called ``self-consistent'', and sometimes
more accurately described as ``asymmetric self-consistent.''
This approach had the drawback
that it overpredicted the effect of cracks on reducing elastic compliance,
and therefore gave a relatively low value 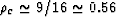 at which the cracked medium would fail. But it is known that failure
does not usually occur at such small crack densities, so these
overall predictions are often criticized on this basis. [See Henyey
and Pomphrey, 1982; Zimmerman, 1991.] Hudson (1980;
1996) used a different method, the so-called ``method of smoothing''
first introduced in the mathematics literature, for the crack problem.
Keeping density corrections just to first order in the Hudson approach
gives an improvement over the previously mentioned scheme. Hudson
also introduced a second order correction, but Sayers and Kachanov
(1991) point out that this approach then violates rigorous Hashin-Shtrikman
upper bounds on the moduli for this problem. They recommend instead using
a differential scheme [see Zimmerman (1991) for an excellent review of the DS],
because the DS tracks Hudson's first order model at low concentration
of cracks, but never violates the HS bounds at high concentrations.
at which the cracked medium would fail. But it is known that failure
does not usually occur at such small crack densities, so these
overall predictions are often criticized on this basis. [See Henyey
and Pomphrey, 1982; Zimmerman, 1991.] Hudson (1980;
1996) used a different method, the so-called ``method of smoothing''
first introduced in the mathematics literature, for the crack problem.
Keeping density corrections just to first order in the Hudson approach
gives an improvement over the previously mentioned scheme. Hudson
also introduced a second order correction, but Sayers and Kachanov
(1991) point out that this approach then violates rigorous Hashin-Shtrikman
upper bounds on the moduli for this problem. They recommend instead using
a differential scheme [see Zimmerman (1991) for an excellent review of the DS],
because the DS tracks Hudson's first order model at low concentration
of cracks, but never violates the HS bounds at high concentrations.