




Next: RMO function with uniform
Up: Biondi: RMO in anisotropic
Previous: Angle-Domain Common Image Gathers
The generalization of kinematic anisotropic migration
and the analysis of the kinematics of the offset-to-angle
transformation presented in the previous section
enables a simple analysis of the residual moveout (RMO)
in ADCIGs caused by errors in anisotropic velocity parameters.
In this section I derive the RMO function by
linearizing the relationship of the imaging depth in the angle
domain with respect to perturbations in the anisotropic parameters.
The linearization is evaluated around the correct migration
velocity function; that is, when the image
in the subsurface-offset domain is well focused at zero offset.
As in the previous section,
I limit my analysis to reflections from flat interfaces.
However, a generalization of the flat-events analysis to
dipping events should be conceptually
straightforward, though not necessarily simple from the analytical
point of view.
Furthermore, I derive relationships assuming that the velocity
perturbations are limited to a homogeneous half-space above the reflector.
The same relationships can be easily adapted to the case of
a homogeneous layer above the reflector by transforming the
depth variable into a relative depth with respect to the top of the layer
under consideration.
At the end of this section I present the fundamental
relationship for broadening the application of the theory
to heterogeneous media.
This relationship links the traveltime perturbations
to the reflector movements
and it can be used in a ray-based tomographic velocity-update procedure.
A VTI velocity function, either group or phase, is described by the following
vector of three velocities 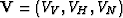 ,or by the corresponding vector of three slownesses
,or by the corresponding vector of three slownesses 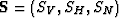 used in equation 36.
I define the perturbations as the combination of one multiplicative factor
for each of the velocities and one multiplicative factor for all velocities;
that is, the perturbed velocity
used in equation 36.
I define the perturbations as the combination of one multiplicative factor
for each of the velocities and one multiplicative factor for all velocities;
that is, the perturbed velocity  is defined as:
is defined as:
| 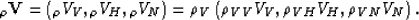 |
(10) |
The velocity-parameter perturbations is thus defined
by the following four-components vector
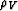 =
=
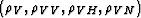 .
.
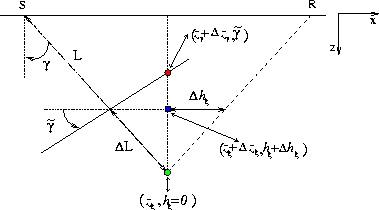
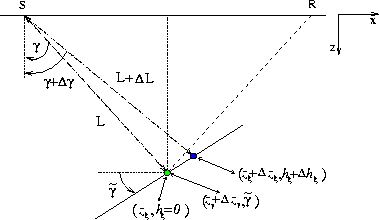
cig-2d-aniso-delta1-flat-v1
Figure 3
Linearized perturbations of the image-point locations
(both in the subsurface-offset domain and the angle domain)
caused by changes in the ray length L,
as evaluated using the first term in equation 11.
|
|  |

cig-2d-aniso-delta2-flat-v1
Figure 4
Linearized perturbations of the image-point locations
(both in the subsurface-offset domain and the angle domain)
caused by changes in the aperture angle  ,as evaluated using the second term in equation 11.
Notice that the image point in the angle domain does not move,
no matter how large the corresponding movement
in the subsurface-offset domain is. ,as evaluated using the second term in equation 11.
Notice that the image point in the angle domain does not move,
no matter how large the corresponding movement
in the subsurface-offset domain is.
|
|  |

Differentiating,
the expression for the depth
of the image point in the angle domain 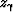 (equation 9)
with respect to the i-th component in the perturbation vector,
we obtain the following:
(equation 9)
with respect to the i-th component in the perturbation vector,
we obtain the following:
| 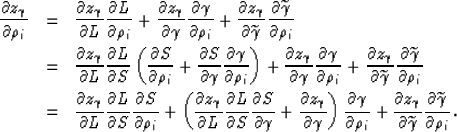 |
(11) |
| (12) |
| (13) |
In Appendix B I demonstrate that the
terms multiplying the partial derivatives
with respect to the angles are zero,
and equation 13 simplifies into:
| 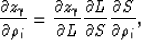 |
(14) |
where
| 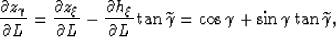 |
(15) |
and
|  |
(16) |
and consequently
| 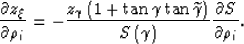 |
(17) |
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) graphically illustrate the image perturbations related to
the first two terms in equation 11.
Figure
graphically illustrate the image perturbations related to
the first two terms in equation 11.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
the movement of the image points (both in the subsurface-offset domain
and the angle domain) caused by changes in the ray length L.
Figure
shows
the movement of the image points (both in the subsurface-offset domain
and the angle domain) caused by changes in the ray length L.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) provides a geometrical explanation of why the second term
in equation 11 vanishes.
It shows
that perturbations in the aperture angle
provides a geometrical explanation of why the second term
in equation 11 vanishes.
It shows
that perturbations in the aperture angle 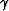 cause
the subsurface-offset domain image point to move
along the tangent to the wavefront (tilted with the phase angle
cause
the subsurface-offset domain image point to move
along the tangent to the wavefront (tilted with the phase angle 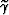 ).
Since this movement is constrained along the tangent,
the image point in the angle domain does not move,
no matter how large the movement in the subsurface-offset domain is.
).
Since this movement is constrained along the tangent,
the image point in the angle domain does not move,
no matter how large the movement in the subsurface-offset domain is.
![]() ,or by the corresponding vector of three slownesses
,or by the corresponding vector of three slownesses ![]() used in equation 36.
I define the perturbations as the combination of one multiplicative factor
for each of the velocities and one multiplicative factor for all velocities;
that is, the perturbed velocity
used in equation 36.
I define the perturbations as the combination of one multiplicative factor
for each of the velocities and one multiplicative factor for all velocities;
that is, the perturbed velocity ![]() is defined as:
is defined as:


![]() (equation 9)
with respect to the i-th component in the perturbation vector,
we obtain the following:
(equation 9)
with respect to the i-th component in the perturbation vector,
we obtain the following:
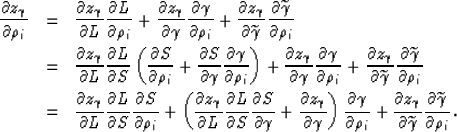

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) graphically illustrate the image perturbations related to
the first two terms in equation 11.
Figure
graphically illustrate the image perturbations related to
the first two terms in equation 11.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
the movement of the image points (both in the subsurface-offset domain
and the angle domain) caused by changes in the ray length L.
Figure
shows
the movement of the image points (both in the subsurface-offset domain
and the angle domain) caused by changes in the ray length L.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) provides a geometrical explanation of why the second term
in equation 11 vanishes.
It shows
that perturbations in the aperture angle
provides a geometrical explanation of why the second term
in equation 11 vanishes.
It shows
that perturbations in the aperture angle ![]() cause
the subsurface-offset domain image point to move
along the tangent to the wavefront (tilted with the phase angle
cause
the subsurface-offset domain image point to move
along the tangent to the wavefront (tilted with the phase angle ![]() ).
Since this movement is constrained along the tangent,
the image point in the angle domain does not move,
no matter how large the movement in the subsurface-offset domain is.
).
Since this movement is constrained along the tangent,
the image point in the angle domain does not move,
no matter how large the movement in the subsurface-offset domain is.