




Next: About this document ...
Up: Biondi: RMO in anisotropic
Previous: Independence of depth perturbations
In this Appendix I present the analytical expressions
for the derivatives of the group slowness function
with respect to the velocity-perturbation parameters
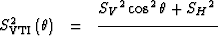 .These derivatives depend
on the particular form chosen to approximate
the slowness function.
In this paper I use following approximation of the VTI slowness function
Fowler (2003):
.These derivatives depend
on the particular form chosen to approximate
the slowness function.
In this paper I use following approximation of the VTI slowness function
Fowler (2003):
| 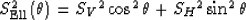 |
|
| (36) |
where
| 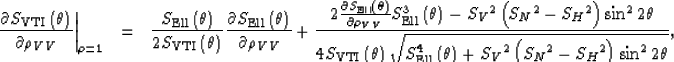 |
(37) |
is the elliptical component.
The derivatives are then written as:
| 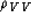 |
(38) |
| (39) |
| (40) |
where the derivatives of the elliptical component with
respect to 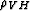 and
and  are:
are:





Next: About this document ...
Up: Biondi: RMO in anisotropic
Previous: Independence of depth perturbations
Stanford Exploration Project
11/1/2005
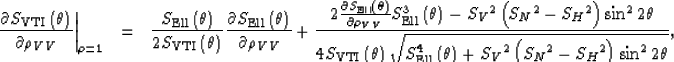
 are:
are: