Next: Two Distinct Gassmann Materials,
Up: FOUR SCENARIOS
Previous: Constant Drained Bulk Modulus,
To add one level of complication, consider next the same porous
framework as before, but now suppose that the saturation is patchy
(White, 1975; Berryman et al., 1998; Norris, 1993;
Dvorkin et al., 1999; Johnson, 2001; Berryman et al., 2002a),
rather than homogeneous. The idea is that some of the layers in the
grains will have a liquid saturant having Kf = Kl, while others
will have a gas saturant having Kf = Kg. In general I assume
that 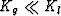 so that for most purposes the gas saturated parts
of the system satisfy
so that for most purposes the gas saturated parts
of the system satisfy 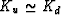 , i.e., undrained moduli are to
a very good approximation the same as the drained moduli for these layers.
If this were not so,
then I could treat the second saturant in exactly the same way as I
will treat the liquid saturant; but there would be no new ideas
required to do this, so I will not stress this approach here.
, i.e., undrained moduli are to
a very good approximation the same as the drained moduli for these layers.
If this were not so,
then I could treat the second saturant in exactly the same way as I
will treat the liquid saturant; but there would be no new ideas
required to do this, so I will not stress this approach here.
For this system, the drained constants are all the same as in the
preceding example. In particular, the overall volume effective stress
coefficient 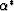 is the same.
is the same.
The undrained constants differ for this system however because the
undrained bulk modulus is not constant in the layers. Gassmann's
formula does not provide an answer for this overall bulk modulus
because the system is not homogeneous. But Backus averaging
determines all the elastic constants in a straightforward way for this system
[see Berryman (2004a)]. The correct results are obtained for all the constants related to
Voigt and Reuss averages [Eqs. (4)-(9)
for both bulk and shear moduli] as long as
the K's shown explicitly in (2) are properly
interpreted as the undrained constants Ku from (17)
for the fluids having bulk moduli Kl or Kg in the appropriate layers.
One explicit result found useful to quote from some earlier work
(Berryman, 2004a) is
| ![\begin{displaymath}
\begin{array}
{cc}
G_{\rm eff}^v = c_{66} - \frac{4c_{33}^u}...
...left<\frac{\Delta\mu}{K_u+ 4\mu/3}\right\gt^2\Big],\end{array} \end{displaymath}](img79.gif) |
(25) |
where 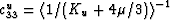 and the bracket
notation has the same meaning as in the Backus formulas (2).
The difference
and the bracket
notation has the same meaning as in the Backus formulas (2).
The difference 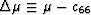 is the deviation of the
layer shear modulus locally from the overall average across all the
layers. The term in square brackets in (25) is always
non-negative. As Ku in the layers ranges (parametrically) from
zero to infinity, the corrections from the square bracket term times
the factor
is the deviation of the
layer shear modulus locally from the overall average across all the
layers. The term in square brackets in (25) is always
non-negative. As Ku in the layers ranges (parametrically) from
zero to infinity, the corrections from the square bracket term times
the factor 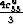 can be shown to decrease from c66-c44 to zero. Thus,
can be shown to decrease from c66-c44 to zero. Thus,
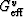 in the layered model ranges for all possible layered
poroelastic systems from c44 to c66.
in the layered model ranges for all possible layered
poroelastic systems from c44 to c66.
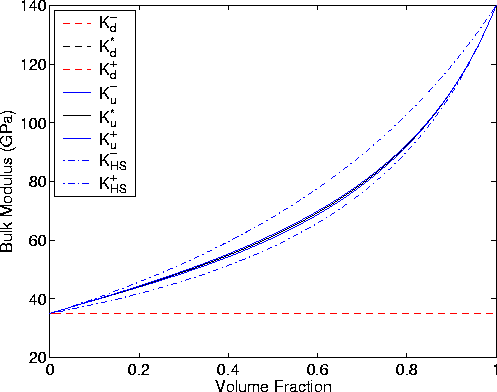
Figure 3 shows that the drained bulk modulus does not change with
volume fraction, since all the layers have the same drained bulk
modulus. The undrained bulk modulus can have some small variations,
however, due to variations in the shear modulus,
as is shown by the small spread in the bulk modulus bounds.
Uncorrelated Hashin-Shtrikman bounds [computed by evaluating
(3) at 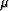 's having the lowest and highest shear modulus
values among all those in the layers] are also shown here for
comparison purposes. Clearly, the Peselnick-Meister-Watt correlated
bounds based on the polycrystals of laminates microstructure are much tighter.
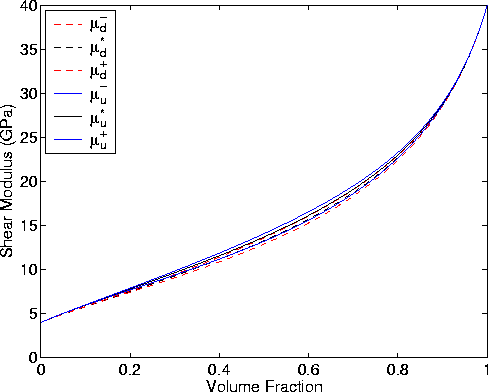
Figure 4 shows that the overall shear modulus has only relatively weak
dependence (though stronger than that in Figure 3)
on patchy saturation when the bulk modulus itself is uniform.
Figure 5 shows that shear modulus changes with saturation, while
small, are present and not very tightly coupled to the bulk modulus
changes (drained to undrained). This observation is seen to be especially
significant at the lowest volume fractions of liquid, as the changes in shear
compliance are greater here (by a factor of about 3) than the corresponding
changes in the bulk compliance.
's having the lowest and highest shear modulus
values among all those in the layers] are also shown here for
comparison purposes. Clearly, the Peselnick-Meister-Watt correlated
bounds based on the polycrystals of laminates microstructure are much tighter.
Figure 4 shows that the overall shear modulus has only relatively weak
dependence (though stronger than that in Figure 3)
on patchy saturation when the bulk modulus itself is uniform.
Figure 5 shows that shear modulus changes with saturation, while
small, are present and not very tightly coupled to the bulk modulus
changes (drained to undrained). This observation is seen to be especially
significant at the lowest volume fractions of liquid, as the changes in shear
compliance are greater here (by a factor of about 3) than the corresponding
changes in the bulk compliance.
Fig3
Figure 3 Illustrating the bulk modulus results for the
random polycrystals of porous laminates model for patchy saturation
when each grain is composed of two
constituents: (1) Kd(1) = 35.0 GPa, 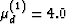 GPa and
(2) Kd(2) = 35.0 GPa,
GPa and
(2) Kd(2) = 35.0 GPa, 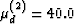 GPa. Skempton's
coefficient is taken to be B = 0.0 for constituent 1 (gas saturated),
and B = 1.0 for constituent 2 (liquid saturated). The
effective stress coefficients for the layers are both given by
GPa. Skempton's
coefficient is taken to be B = 0.0 for constituent 1 (gas saturated),
and B = 1.0 for constituent 2 (liquid saturated). The
effective stress coefficients for the layers are both given by
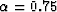 , so
, so 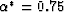 also. Porosity does not play
a direct role in the
calculation when we are using B as the fluid substitution parameter.
Volume fraction of the layers varies from 0 to 100% of constituent number 2.
To emphasize the tightness of the polycrystal (correlated) bounds,
uncorrelated Hashin-Shtrikman bounds
also. Porosity does not play
a direct role in the
calculation when we are using B as the fluid substitution parameter.
Volume fraction of the layers varies from 0 to 100% of constituent number 2.
To emphasize the tightness of the polycrystal (correlated) bounds,
uncorrelated Hashin-Shtrikman bounds 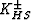 on the undrained
bulk modulus are also shown.
on the undrained
bulk modulus are also shown.

Fig4
Figure 4 Illustrating the shear modulus results
for the random polycrystals of porous laminates model. Model
parameters are the same as in Figure 3 for patchy saturation.

Fig5
Figure 5 Plot of the ratio R from equation (24),
being the ratio of compliance differences due to fluid saturation.
These results are for the same model described in Figure 3
for patchy saturation.
The values of R should be compared to those predicted by Mavko
and Jizba (1991) for very low porosity and flat cracks,
when 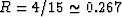 . We find in contrast
that, for partial and patchy saturation, R can take any positive
value, or zero.
. We find in contrast
that, for partial and patchy saturation, R can take any positive
value, or zero.






Next: Two Distinct Gassmann Materials,
Up: FOUR SCENARIOS
Previous: Constant Drained Bulk Modulus,
Stanford Exploration Project
5/3/2005
![]() is the same.
is the same.
![\begin{displaymath}
\begin{array}
{cc}
G_{\rm eff}^v = c_{66} - \frac{4c_{33}^u}...
...left<\frac{\Delta\mu}{K_u+ 4\mu/3}\right\gt^2\Big],\end{array} \end{displaymath}](img79.gif)
![]() 's having the lowest and highest shear modulus
values among all those in the layers] are also shown here for
comparison purposes. Clearly, the Peselnick-Meister-Watt correlated
bounds based on the polycrystals of laminates microstructure are much tighter.
Figure 4 shows that the overall shear modulus has only relatively weak
dependence (though stronger than that in Figure 3)
on patchy saturation when the bulk modulus itself is uniform.
Figure 5 shows that shear modulus changes with saturation, while
small, are present and not very tightly coupled to the bulk modulus
changes (drained to undrained). This observation is seen to be especially
significant at the lowest volume fractions of liquid, as the changes in shear
compliance are greater here (by a factor of about 3) than the corresponding
changes in the bulk compliance.
's having the lowest and highest shear modulus
values among all those in the layers] are also shown here for
comparison purposes. Clearly, the Peselnick-Meister-Watt correlated
bounds based on the polycrystals of laminates microstructure are much tighter.
Figure 4 shows that the overall shear modulus has only relatively weak
dependence (though stronger than that in Figure 3)
on patchy saturation when the bulk modulus itself is uniform.
Figure 5 shows that shear modulus changes with saturation, while
small, are present and not very tightly coupled to the bulk modulus
changes (drained to undrained). This observation is seen to be especially
significant at the lowest volume fractions of liquid, as the changes in shear
compliance are greater here (by a factor of about 3) than the corresponding
changes in the bulk compliance.