Next: Two Distinct Gassmann Materials,
Up: FOUR SCENARIOS
Previous: Constant Drained Bulk Modulus,
This example and the next one will remove the restriction that the
porous frame material is uniform. To have as much control as possible,
we limit the heterogeneity to just two types of drained bulk moduli,
Kd(1) and Kd(2). These occur with a frequency measured by the
volume fractions f1 and f2, respectively. These porous
materials fill the space, so f1 + f2 = 1. The effective
stress coefficient is known exactly for this model and is given by
(20). This result is true both for homogeneously
saturated two-component media (Berryman and Milton, 1991)
as treated in this
example, or for the type of patchy saturation treated in the next
example. Proof of this statement is provided in Appendix A.
For Gassmann's equations in each material,
we also need either the fluid bulk modulus together with
the layer porosities  and
and 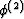 , or we just need
the Skempton coefficient, B. For simplicity, we take B = 0.0 for
uniform gas saturation, and B = 1.0 for uniform liquid saturation.
(Although B = 1 may not be exactly correct for real liquid-saturated
reservoirs, only the product
, or we just need
the Skempton coefficient, B. For simplicity, we take B = 0.0 for
uniform gas saturation, and B = 1.0 for uniform liquid saturation.
(Although B = 1 may not be exactly correct for real liquid-saturated
reservoirs, only the product 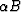 is important for the modeling
examples that follow. So desired differences in B can be introduced
through differences in
is important for the modeling
examples that follow. So desired differences in B can be introduced
through differences in  . In this way we hope to capture the
essence of this problem using the minimum number of free parameters.) This
summarizes the part of the modeling that is the same in this
example and the next.
. In this way we hope to capture the
essence of this problem using the minimum number of free parameters.) This
summarizes the part of the modeling that is the same in this
example and the next.
We will now assume that the fluid saturation is uniform throughout the
stated model material: (1l,2l). [Notation indicates first layer is
liquid filled (l) and second layer is also liquid filled. The
alternative is that some layers are gas filled (g).]
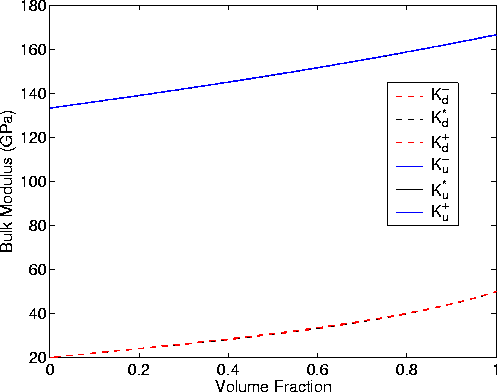
In Figure 6 there appear to be only two curves for bulk modulus,
but in fact six curves are plotted here. All three of the drained
curves are so close to each other that they cannot be distinguished
on the scale of this plot.
Similarly, all three of the undrained curves are equally
indistinguishable.
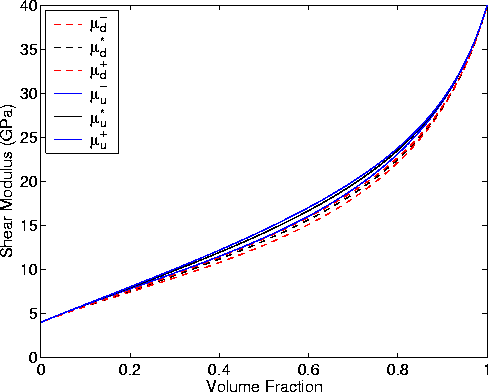
Figure 7 appears to be both qualitatively and quantitatively very
similar to Figure 1. But this time we find the inequality
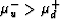 is never violated. So there is no doubt that
shear modulus is affected by pore fluids in this system.
is never violated. So there is no doubt that
shear modulus is affected by pore fluids in this system.
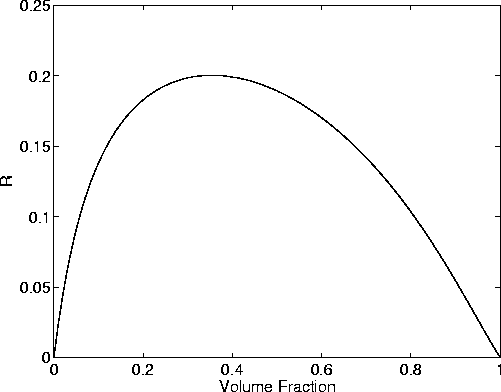
Figure 8 shows that the maximum value of 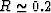 occurs around
occurs around
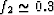 . For this case, 4/15 is an upper bound on R, but
I know this is not a general result.
. For this case, 4/15 is an upper bound on R, but
I know this is not a general result.
Fig6
Figure 6 Illustrating the bulk modulus results
for the random polycrystals of porous laminates model for
homogeneous saturation when each grain is composed of two
constituents: (1) Kd(1) = 20.0 GPa, 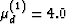 GPa and
(2) Kd(2) = 50.0 GPa,
GPa and
(2) Kd(2) = 50.0 GPa, 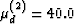 GPa. Skempton's
coefficient is taken to be B = 0.0 when the system is gas saturated,
and B = 1.0 when the system is fully liquid saturated. The
effective stress coefficients for the layers are, respectively,
GPa. Skempton's
coefficient is taken to be B = 0.0 when the system is gas saturated,
and B = 1.0 when the system is fully liquid saturated. The
effective stress coefficients for the layers are, respectively,
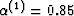 and
and 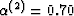 . Porosity does not
play a direct role in the calculation when we are using B as the fluid
substitution parameter. Volume fraction of the layers varies from
0 to 100% of constituent number 2.
. Porosity does not
play a direct role in the calculation when we are using B as the fluid
substitution parameter. Volume fraction of the layers varies from
0 to 100% of constituent number 2.

Fig7
Figure 7 Illustrating the shear modulus results
for the random polycrystals of porous laminates model. Model
parameters are the same as in Figure 6 for homogeneous saturation.

Fig8
Figure 8 Plot of the ratio R from equation (24),
being the ratio of compliance differences due to fluid saturation.
These results are for the same model described in Figure 6
for homogeneous saturation.
The values of R should be compared to those predicted by Mavko
and Jizba (1991) for very low porosity and flat cracks,
when 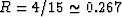 . We find in contrast
that the random polycrystals of porous laminates model for the case
considered always has
. We find in contrast
that the random polycrystals of porous laminates model for the case
considered always has 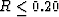 .
.






Next: Two Distinct Gassmann Materials,
Up: FOUR SCENARIOS
Previous: Constant Drained Bulk Modulus,
Stanford Exploration Project
5/3/2005
![]() is never violated. So there is no doubt that
shear modulus is affected by pore fluids in this system.
is never violated. So there is no doubt that
shear modulus is affected by pore fluids in this system.
![]() occurs around
occurs around
![]() . For this case, 4/15 is an upper bound on R, but
I know this is not a general result.
. For this case, 4/15 is an upper bound on R, but
I know this is not a general result.