Next: Constant Drained Bulk Modulus,
Up: FOUR SCENARIOS
Previous: FOUR SCENARIOS
For assumed constant isotropic drained bulk modulus, we have
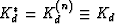 for all N layers as well as the overall
medium, and when N=2 we can prove easily using (20) that
for all N layers as well as the overall
medium, and when N=2 we can prove easily using (20) that
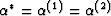 . When the fluid is uniform
throughout the medium, the undrained bulk moduli also satisfy
. When the fluid is uniform
throughout the medium, the undrained bulk moduli also satisfy
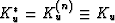 , since Gassmann's equation depends only on
constants that are uniform throughout this model material.
Now it has been shown previously (Berryman, 2004b) that when the drained bulk modulus is uniform, a general result
for
, since Gassmann's equation depends only on
constants that are uniform throughout this model material.
Now it has been shown previously (Berryman, 2004b) that when the drained bulk modulus is uniform, a general result
for 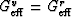 is
is
| ![\begin{displaymath}
G^v_d = \left[\sum_{n=1}^N \frac{f_n}{\mu_n + 3K_d/4}\right]^{-1} - 3K_d/4,
\end{displaymath}](img54.gif) |
(21) |
fn being the volume fraction of the layers.
This result follows easily from the Backus averages presented in
(2) and the formula for 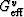 in (6).
In the presence of pore fluid and since each layer is a Gassmann
material, the shear moduli of the individual porous layers do not
change. So, a second result of the same type is available for the undrained
uniaxial shear energy per unit volume
in (6).
In the presence of pore fluid and since each layer is a Gassmann
material, the shear moduli of the individual porous layers do not
change. So, a second result of the same type is available for the undrained
uniaxial shear energy per unit volume 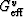 in this medium:
in this medium:
| ![\begin{displaymath}
G^v_u = \left[\sum_{n=1}^N \frac{f_n}{\mu_n + 3K_u/4}\right]^{-1} - 3K_u/4,
\end{displaymath}](img56.gif) |
(22) |
fn again being the volume fraction of the layers.
Neither of these two shear contributions is the overall modulus. They
are just contributions of the uniaxial shear component (within each laminated
grain) as defined earlier. However, they can be substituted for the term
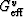 in the Peselnick-Meister-Watt bounds defined by
(15). Note that it is easy to show from the forms of
(21) and (22) that
in the Peselnick-Meister-Watt bounds defined by
(15). Note that it is easy to show from the forms of
(21) and (22) that 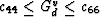 ,and similarly that
,and similarly that 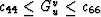 . [Furthermore, since
. [Furthermore, since
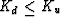 and the functionals in (21) and (22)
vary monotonically with their arguments Kd and Ku, it is easy to
see that
and the functionals in (21) and (22)
vary monotonically with their arguments Kd and Ku, it is easy to
see that 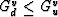 .] Thus, from
(12) and (13), the best
choices for shear moduli of the comparison materials are always
given by
G- = c44 and G+ = c66 for this particular model material.
So
.] Thus, from
(12) and (13), the best
choices for shear moduli of the comparison materials are always
given by
G- = c44 and G+ = c66 for this particular model material.
So 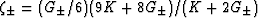 in (15),
where K takes the values K = Kd for the drained case and
K = Ku for the undrained case. In both cases, KR = KV = K since the
drained bulk modulus is uniform, so the form of the shear modulus bounds in
(15) also simplifies to
in (15),
where K takes the values K = Kd for the drained case and
K = Ku for the undrained case. In both cases, KR = KV = K since the
drained bulk modulus is uniform, so the form of the shear modulus bounds in
(15) also simplifies to
| ![\begin{displaymath}
\frac{1}{\mu^\pm + \zeta_\pm} =
\frac{1}{5}\left[\frac{1}
{...
...rac{2}{c_{44}+\zeta_\pm} + \frac{2}{c_{66}+\zeta_\pm}\right].
\end{displaymath}](img62.gif) |
(23) |
We now have upper and lower bounds on the shear modulus in both
drained and undrained circumstances by using the appropriate values of
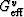 and
and 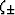 for each case. It is also possible to
generate self-consistent estimates (Berryman, 2004b) for these moduli directly from the
form of these bounds by instead making the substitutions
for each case. It is also possible to
generate self-consistent estimates (Berryman, 2004b) for these moduli directly from the
form of these bounds by instead making the substitutions
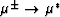 and
and 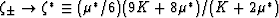 . The results of all these formulas
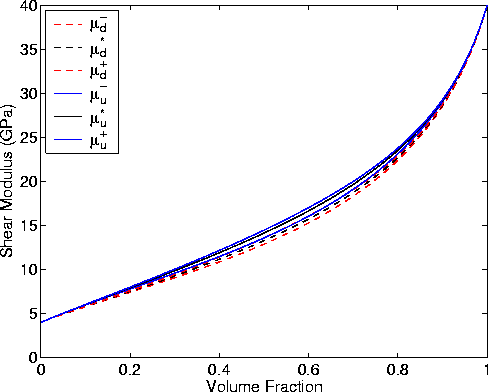
are illustrated in Figure 1.
. The results of all these formulas
are illustrated in Figure 1.
Another important concept in these analyses will be the ratio
of compliance differences defined by
| 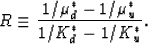 |
(24) |
This quantity has been defined and discussed previously by
Berryman et al. (2002b). It is most useful for determining the extent to which an
identity derived by Mavko and Jizba (1991) for very low porosity media containing randomly
oriented fractures is either satisfied or violated by other
types of porous media. For the case studied by Mavko and Jizba (1991),
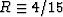 . However, it has been shown that
for penny-shaped cracks at finite porosities R can be either higher or
lower than 4/15, and furthermore that the factor R tends to zero
when the pores approach spherical shapes (aspect ratio
. However, it has been shown that
for penny-shaped cracks at finite porosities R can be either higher or
lower than 4/15, and furthermore that the factor R tends to zero
when the pores approach spherical shapes (aspect ratio 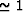 )[see Goertz and Knight (1998) and Berryman et al. (2002b)].
So this ratio is a sensitive measure of the dependence of
)[see Goertz and Knight (1998) and Berryman et al. (2002b)].
So this ratio is a sensitive measure of the dependence of
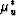 on the fluid content of a porous medium, and also to some
extent on the microgeometry of the pores.
on the fluid content of a porous medium, and also to some
extent on the microgeometry of the pores.
Figure 1 shows that, for most choices of volume fractions, the drained
and undrained values of shear modulus bounds do not overlap. Clearly, as the
volume fractions approach zero or unity, the system approaches a pure
Gassmann system; but, away from these limiting cases, the results
are both qualitatively and quantitatively different from Gassmann's
predictions. Graphically speaking, it appears that the lower bound
of the undrained constant is always greater than the upper bound on
the drained constants,
i.e., 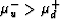 . But, when this figure is magnified, we
find there are small regions of volume fraction where this inequality
is violated slightly. So there is still little doubt that
shear modulus is affected by pore fluids in these systems,
and for some ranges of volume fraction there is no doubt.
This result is a clear indication that Gassmann's results
for shear are not generally valid for this model - as expected.
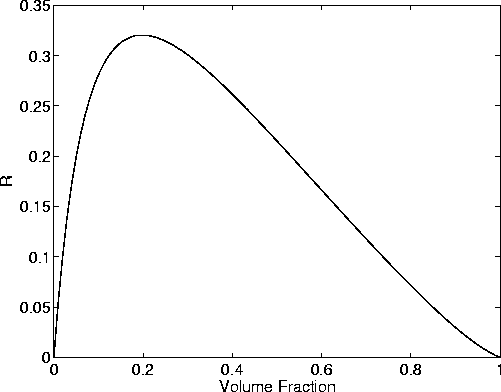
Figure 2 shows that the maximum value of R for this case
occurs around
. But, when this figure is magnified, we
find there are small regions of volume fraction where this inequality
is violated slightly. So there is still little doubt that
shear modulus is affected by pore fluids in these systems,
and for some ranges of volume fraction there is no doubt.
This result is a clear indication that Gassmann's results
for shear are not generally valid for this model - as expected.
Figure 2 shows that the maximum value of R for this case
occurs around 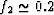 . Furthermore,
the magnitude of this value is about 0.32, and therefore
greater than 4/15. This shows again [as was shown previously by
Berryman et al. (2002b)] that R = 4/15 is also not in general an upper bound on R.
. Furthermore,
the magnitude of this value is about 0.32, and therefore
greater than 4/15. This shows again [as was shown previously by
Berryman et al. (2002b)] that R = 4/15 is also not in general an upper bound on R.
Fig1
Figure 1 Illustrating the shear modulus results
for the random polycrystals of porous laminates model for
homogeneous saturation when each grain is composed of two
constituents: (1) Kd(1) = 35.0 GPa, 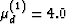 GPa and
(2) Kd(2) = 35.0 GPa,
GPa and
(2) Kd(2) = 35.0 GPa, 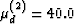 GPa. Skempton's
coefficient is taken to be B = 0.0 when the system is gas saturated,
and B = 1.0 when the system is fully liquid saturated. The
effective stress coefficients for the layers are both
GPa. Skempton's
coefficient is taken to be B = 0.0 when the system is gas saturated,
and B = 1.0 when the system is fully liquid saturated. The
effective stress coefficients for the layers are both
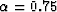 , and
, and 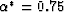 also.
The computed undrained bulk modulus is Ku = 140 GPa.
Volume fraction of the layers varies from
0 to 100% of constituent number 2.
also.
The computed undrained bulk modulus is Ku = 140 GPa.
Volume fraction of the layers varies from
0 to 100% of constituent number 2.

Fig2
Figure 2 Plot of the ratio R from equation (24),
being the ratio of compliance differences due to fluid saturation.
These results are for the same model described in Figure 1
for homogeneous saturation.
The values of R should be compared to those predicted by Mavko
and Jizba (1991) for very low porosity and flat cracks,
when 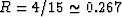 . We find in contrast
that the random polycrystals of porous laminates model for the case
considered always has
. We find in contrast
that the random polycrystals of porous laminates model for the case
considered always has 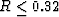 .
.






Next: Constant Drained Bulk Modulus,
Up: FOUR SCENARIOS
Previous: FOUR SCENARIOS
Stanford Exploration Project
5/3/2005
![\begin{displaymath}
G^v_d = \left[\sum_{n=1}^N \frac{f_n}{\mu_n + 3K_d/4}\right]^{-1} - 3K_d/4,
\end{displaymath}](img54.gif)
![\begin{displaymath}
G^v_d = \left[\sum_{n=1}^N \frac{f_n}{\mu_n + 3K_d/4}\right]^{-1} - 3K_d/4,
\end{displaymath}](img54.gif)
![\begin{displaymath}
G^v_u = \left[\sum_{n=1}^N \frac{f_n}{\mu_n + 3K_u/4}\right]^{-1} - 3K_u/4,
\end{displaymath}](img56.gif)
![]() in the Peselnick-Meister-Watt bounds defined by
(15). Note that it is easy to show from the forms of
(21) and (22) that
in the Peselnick-Meister-Watt bounds defined by
(15). Note that it is easy to show from the forms of
(21) and (22) that ![]() ,and similarly that
,and similarly that ![]() . [Furthermore, since
. [Furthermore, since
![]() and the functionals in (21) and (22)
vary monotonically with their arguments Kd and Ku, it is easy to
see that
and the functionals in (21) and (22)
vary monotonically with their arguments Kd and Ku, it is easy to
see that ![]() .] Thus, from
(12) and (13), the best
choices for shear moduli of the comparison materials are always
given by
G- = c44 and G+ = c66 for this particular model material.
So
.] Thus, from
(12) and (13), the best
choices for shear moduli of the comparison materials are always
given by
G- = c44 and G+ = c66 for this particular model material.
So ![]() in (15),
where K takes the values K = Kd for the drained case and
K = Ku for the undrained case. In both cases, KR = KV = K since the
drained bulk modulus is uniform, so the form of the shear modulus bounds in
(15) also simplifies to
in (15),
where K takes the values K = Kd for the drained case and
K = Ku for the undrained case. In both cases, KR = KV = K since the
drained bulk modulus is uniform, so the form of the shear modulus bounds in
(15) also simplifies to
![]() . But, when this figure is magnified, we
find there are small regions of volume fraction where this inequality
is violated slightly. So there is still little doubt that
shear modulus is affected by pore fluids in these systems,
and for some ranges of volume fraction there is no doubt.
This result is a clear indication that Gassmann's results
for shear are not generally valid for this model - as expected.
Figure 2 shows that the maximum value of R for this case
occurs around
. But, when this figure is magnified, we
find there are small regions of volume fraction where this inequality
is violated slightly. So there is still little doubt that
shear modulus is affected by pore fluids in these systems,
and for some ranges of volume fraction there is no doubt.
This result is a clear indication that Gassmann's results
for shear are not generally valid for this model - as expected.
Figure 2 shows that the maximum value of R for this case
occurs around ![]() . Furthermore,
the magnitude of this value is about 0.32, and therefore
greater than 4/15. This shows again [as was shown previously by
Berryman et al. (2002b)] that R = 4/15 is also not in general an upper bound on R.
. Furthermore,
the magnitude of this value is about 0.32, and therefore
greater than 4/15. This shows again [as was shown previously by
Berryman et al. (2002b)] that R = 4/15 is also not in general an upper bound on R.