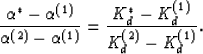Next: FOUR SCENARIOS
Up: Berryman: Geomechanical constants of
Previous: Hashin-Shtrikman Bounds
My main focus here will be the extension of earlier work in
elasticity to the case of locally layered poroelastic media
(Wang, 2000; Coussy, 2004),
where the laminated grains (or crystals) are formed by sequential
layering of N porous isotropic layers.
Although these grains each have the same quasi-static anisotropic
elastic behavior, they do not necessarily have the same shapes or the same
orientations of their crystal symmetry axes. Specifically, we want
to study the case of isotropic random polycrystals, wherein the
individuals can and do take on all possible orientations of their
symmetry axes (equiaxed, statistically isotropic polycrystals)
so that the overall composite polycrystal has isotropic
behavior at the macroscopic level. Furthermore, in some
applications, the pores of some grain layers may be filled with different
fluids (heterogeneous saturation conditions)
than those in other layers. This model may or may not be a
realistic one for any given fluid-bearing reservoir whose geomechanics
we need to model. My first goal is arrive at a model for which many of the
available modern tools of elastic and poroelastic
analysis apply, including Hashin-Shtrikman bounds
for a reservoir having isotropic constituents
(Hashin and Shtrikman, 1962a,b,c; 1963a,b),
Peselnick-Meister-Watt
bounds for random polycrystals (Peselnick and Meister, 1965; Watt and
Peselnick, 1980), certain exact relationships known for two-component poroelastic
media (Berryman and Milton, 1991),
and -- whenever
appropriate -- self-consistent or other effective medium estimates
of both elastic constants and conductivities (electrical, thermal,
and hydraulic). By constructing such a model material, we expect to
be able to make estimates of the behavior of the system and at the same
time be able to predict the range of variation likely to be observed
around these estimates, as well as identifying what material and
microgeometry properties control those variations. My further goal
is to be able to make fairly precise
statements about this model that are then useful to our (both mine and
the reader's) intuition
and to quantify how much is really known about these complex systems. In
particular, the hope is to identify assumptions currently and commonly
used in the literature without much apparent justification and
to provide a means of either verifying or falsifying these assumptions
in the context of this model -- if that proves to be possible.
Two distinct results that will be required from poroelasticity theory
are: (a) Gassmann's equations and (b) certain relationships that determine
the overall effective stress coefficient of a composite
poroelastic medium when it is composed of two porous materials
satisfying Gassmann's assumptions. Gassmann's results
(Gassmann, 1951; Berryman, 1999; Wang, 2000)
for the undrained bulk (K) and shear (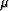 ) moduli of
microhomogeneous (one solid constituent) porous media are:
) moduli of
microhomogeneous (one solid constituent) porous media are:
| 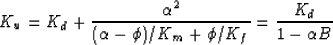 |
(17) |
and
| 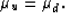 |
(18) |
Here, Ku and 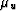 are the undrained (pore fluid trapped)
constants, while Kd and
are the undrained (pore fluid trapped)
constants, while Kd and 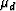 are the drained (pore fluid
untrapped) constants. Porosity (void volume fraction) is
are the drained (pore fluid
untrapped) constants. Porosity (void volume fraction) is 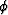 .Grain bulk and shear moduli of the sole mineral constituent are
Km and
.Grain bulk and shear moduli of the sole mineral constituent are
Km and 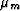 . The bulk modulus of the pore fluid is Kf.
The factor
. The bulk modulus of the pore fluid is Kf.
The factor  is the Biot-Willis (Biot and Willis, 1957) or volume effective stress coefficient
(Nur and Byerlee, 1971; Berryman, 1992; Gurevich, 2004),
related to Km and Kd within each layer by
is the Biot-Willis (Biot and Willis, 1957) or volume effective stress coefficient
(Nur and Byerlee, 1971; Berryman, 1992; Gurevich, 2004),
related to Km and Kd within each layer by
| 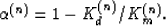 |
(19) |
Skempton's coefficient (Skempton, 1954) is B in (17).
Although my presentation is based on quasi-static results, my
ultimate interest is often applications to seismic wave propagation. In such
circumstances a slightly different terminology is used by some authors
(Mavko and Jizba, 1991). In particular, for high frequency wave propagation,
fluid may be effectively trapped in the pores as it is unable to
equilibrate through pore-pressure diffusion on the time scale of wave
passage. In this case, the term ``unrelaxed'' is sometimes used
instead of ``undrained.''
We will not make any further issue of this
distinction here and stick to the single term ``undrained'' for both
types of applications.
For a porous medium composed of only two constituent porous media, each of
which is microhomogeneous and obeys Gassmann's equations, the exact
relation (Berryman and Milton, 1991) that determines the overall effective stress coefficient
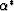 - assuming only that the constituents are in welded
contact (volume fractions and spatial distribution of constituents do not
directly affect the result) - is:
- assuming only that the constituents are in welded
contact (volume fractions and spatial distribution of constituents do not
directly affect the result) - is:
| 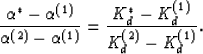 |
(20) |
Here K*d is the overall drained bulk modulus of the composite
system, and the superscripts (1) and (2) reference the
two distinct components in the composite porous medium.





Next: FOUR SCENARIOS
Up: Berryman: Geomechanical constants of
Previous: Hashin-Shtrikman Bounds
Stanford Exploration Project
5/3/2005
![]() ) moduli of
microhomogeneous (one solid constituent) porous media are:
) moduli of
microhomogeneous (one solid constituent) porous media are:
![]() - assuming only that the constituents are in welded
contact (volume fractions and spatial distribution of constituents do not
directly affect the result) - is:
- assuming only that the constituents are in welded
contact (volume fractions and spatial distribution of constituents do not
directly affect the result) - is: