Seismic-wave illumination becomes increasingly problematic in regions with rugged topography and complex geological structure with severe lateral velocity variations. In these hostile cases, we think that seismic-wave illumination is much more important than seismic-data regularization. Without enough illumination for the target reflectors, regular seismic data can not guarantee a quality image.
Seismic-wave illumination is related to the macro-velocity model and the acquisition configuration, both of which are embodied in the Green's function. In fact, seismic-wave illumination analysis inherently is an issue of seismic-wave propagation and observation in the presence of complex velocity structure. Whether a seismic wave reaches a target reflector and whether the reflected wave is received are both important.
() analyze seismic-wave illumination with Beamlet Propagators. With directional illumination maps, the illumination of a reflector is demonstrated. (, ) discuss how the imaging resolution and amplitude are affected by the acquisition geometries with focal beams: emission-focusing and detection-focusing. However, neither methods deals with the compensation for illumination deficiency from the perspective of inverse imaging.
In least-squares inversion theory, the Hessian matrix--the second-order derivatives of the wavefield about the perturbation of a physical parameter--is given. The Hessian matrix is closely related to the seismic-wave illumination of a target reflector.
The two important issues of seismic-wave illumination analysis are (1) compensating for illumination deficiencies and (2) evaluating acquisition patterns and guiding their design.
Seismic-wave migration imaging can be represented by the following matrix equation:
| |
(28) |
| |
(29) |
| |
(30) |
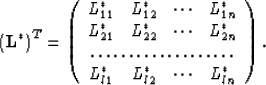 |
(31) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is the Kirchhoff integral migration formula expressed in matrix form.
) is the Kirchhoff integral migration formula expressed in matrix form.
However, if seismic-wave illumination is considered, the concept of double focusing (emission focusing and detection focusing) should be introduced into the general migration-imaging formula (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), following Berkhout's notation (, ):
), following Berkhout's notation (, ):
| |
(32) |
Defining ![]() and
and ![]() gives us the formulae for detection focusing and emission focusing, respectively. Together, they represent the illumination of a point on a reflector.
gives us the formulae for detection focusing and emission focusing, respectively. Together, they represent the illumination of a point on a reflector.
We will analyze the seismic-wave illumination of a target reflector with the local Hessian matrix and compare this with the double-focusing approaches.