




Next: Seismic wave illumination analysis
Up: Seismic data preprocessing
Previous: Common-offset prestack time migration
From the discretized data space, the discretized model space, and their relation formula,
| 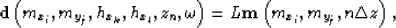 |
(23) |
some causes of aliasing can be clearly seen. The sources of aliasing can be divided into the following three types:
(1) Overly coarse sampling intervals. For example, 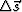 and/or
and/or 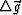 ,
, 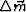 and/or
and/or 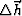 are too coarse, where
are too coarse, where 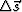 and
and 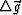 are the shot-point and receiver-point intervals respectively, and
are the shot-point and receiver-point intervals respectively, and 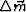 and
and 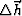 are the CMP and half-offset intervals, respectively.
are the CMP and half-offset intervals, respectively.
(2) Unsuitable modeling or imaging operators, such as the integrated DMO operator (), or the Kirchhoff integral operator (, , , ).
(3) Insufficient output resolution, where the output spatial intervals, such as 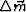 and
and 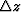 are too coarse.
We can analyze the aliasing in the cases of shot-gather migration, receiver-gather migration, common-offset gather migration, and midpoint half-offset domain migration.
are too coarse.
We can analyze the aliasing in the cases of shot-gather migration, receiver-gather migration, common-offset gather migration, and midpoint half-offset domain migration.
Aliasing in shot gather migration is described by the following equation:
| 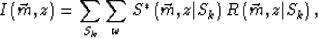 |
(24) |
where 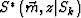 is the conjugate of the extrapolated shot wave-field;
is the conjugate of the extrapolated shot wave-field; 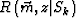 is the extrapolated receiver wave-field. Sk stands for the Kth common-shot gather. In general, single common-shot-gather imaging presents no aliasing, because the receiver-point interval is easily arranged regularly and small enough. However, imaging an entire 2D line or 3D area will present severe aliasing problems because of the irregular and large shot-point intervals.
is the extrapolated receiver wave-field. Sk stands for the Kth common-shot gather. In general, single common-shot-gather imaging presents no aliasing, because the receiver-point interval is easily arranged regularly and small enough. However, imaging an entire 2D line or 3D area will present severe aliasing problems because of the irregular and large shot-point intervals.
Aliasing in receiver-gather migration is described by the following equation:
| 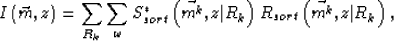 |
(25) |
where 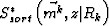 is the extrapolated so-called shot wavefield, which corresponds to a specific receiver point;
is the extrapolated so-called shot wavefield, which corresponds to a specific receiver point; 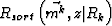 is the extrapolated receiver wavefield, which is sorted from shot gathers. Rk stands for the Kth
common-receiver-gather. In general, single common-receiver-gather imaging profiles are susceptible to aliasing.
is the extrapolated receiver wavefield, which is sorted from shot gathers. Rk stands for the Kth
common-receiver-gather. In general, single common-receiver-gather imaging profiles are susceptible to aliasing.
Aliasing in midpoint half-offset domain migration follows equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
| 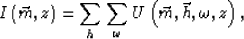 |
(26) |
where 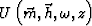 is the extrapolated wavefield with a double-square-root equation. Aliasing will result if
is the extrapolated wavefield with a double-square-root equation. Aliasing will result if 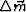 and/or
and/or 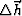 are too coarse.
are too coarse.
Aliasing in common-offset-gather migration is described by the following equation:
| 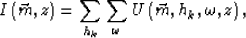 |
(27) |
where 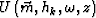 is the extrapolated wavefield with a double-square-root equation. Aliasing will result if
is the extrapolated wavefield with a double-square-root equation. Aliasing will result if 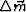 is too coarse.
is too coarse.
In the case of rugged topography, the geometry of the acquisition configuration becomes more and more irregular, especially the shot-point coordinates. Therefore, antialiasing processing is necessary in redatuming, seismic data regularization and migration imaging for land-data imaging.





Next: Seismic wave illumination analysis
Up: Seismic data preprocessing
Previous: Common-offset prestack time migration
Stanford Exploration Project
5/3/2005
![]() and/or
and/or ![]() ,
, ![]() and/or
and/or ![]() are too coarse, where
are too coarse, where ![]() and
and ![]() are the shot-point and receiver-point intervals respectively, and
are the shot-point and receiver-point intervals respectively, and ![]() and
and ![]() are the CMP and half-offset intervals, respectively.
are the CMP and half-offset intervals, respectively.
![]() and
and ![]() are too coarse.
We can analyze the aliasing in the cases of shot-gather migration, receiver-gather migration, common-offset gather migration, and midpoint half-offset domain migration.
are too coarse.
We can analyze the aliasing in the cases of shot-gather migration, receiver-gather migration, common-offset gather migration, and midpoint half-offset domain migration.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):