




Next: Common-offset prestack time migration
Up: Wang and Shan: Imaging
Previous: relationship between data space
As discussed above, seismic-wave imaging needs a suitable data set. In general cases, real data sets have some drawbacks. For example, the spatial sampling of land data commonly is too coarse and/or irregular; marine data sets commonly show feathering. Therefore, seismic-data preprocessing is necessary. Seismic-data preprocessing deals with the signal-to-noise enhancement, wavelet correction, seismic-data regularization and interpolation, and redatuming. The latter three terms are closely related to seismic-wave imaging. Seismic data regularization, interpolation and redatuming can be seen as a seismic-data mapping under the least-squares theory.
An irregular seismic-data set from on-site field acquisition can be expressed as follows:
| 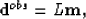 |
(2) |
where L is an ideal seismic-wave propagator, and 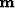 is an ideal underground medium model.
From the irregular observed seismic-data, an underground medium model can be estimated:
is an ideal underground medium model.
From the irregular observed seismic-data, an underground medium model can be estimated:
| ![\begin{displaymath}
\hat{\textbf{m}}_{inv}=\left[\left( \hat{L}^{*}\right)^{T}\hat{L} \right]^{-1}\left( \hat{L}^{*}\right) ^{T}\textbf{d}^{obs}\end{displaymath}](img18.gif) |
(3) |
where 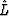 is the practical seismic wave propagator, which can be written as a complex matrix.
is the practical seismic wave propagator, which can be written as a complex matrix. 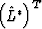 is a conjugate transpose matrix of the matrix
is a conjugate transpose matrix of the matrix 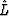 .Substituting the estimated model into equation (
.Substituting the estimated model into equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the estimated and regular data set can be found:
), the estimated and regular data set can be found:
| ![\begin{displaymath}
\hat{\textbf{d}}_{reg}=L\left[\left( \hat{L}^{*}\right)^{T}\hat{L} \right]^{-1}\left( \hat{L}^{*}\right) ^{T}\textbf{d}^{obs}.\end{displaymath}](img21.gif) |
(4) |
In equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the ideal wave propagator L is unknown, but it can be replaced with the practical wave propagator
), the ideal wave propagator L is unknown, but it can be replaced with the practical wave propagator 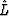 .Therefore, equation (
.Therefore, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be rewritten as
) can be rewritten as
| 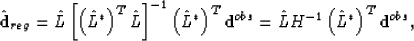 |
(5) |
where 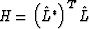 is a Hessian matrix which acts as a filter. If we choose the filter as an ideal full-pass one, that is,
is a Hessian matrix which acts as a filter. If we choose the filter as an ideal full-pass one, that is, 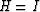 , equation (
, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be rewritten as
) can be rewritten as
| 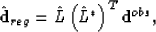 |
(6) |
which is a general seismic data mapping frame. Up to now, the seismic data mapping can be implemented with 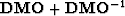 or
or 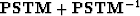 (, , , ).
(, , , ).
Redatuming also can be carried out with equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The formula for redatuming should be modified as follows:
). The formula for redatuming should be modified as follows:
| 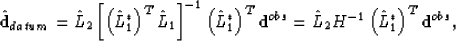 |
(7) |
where 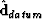 is a new and regular data set extrapolated from a topographic surface to another surface which may be a horizontal or non-horizontal datum.
is a new and regular data set extrapolated from a topographic surface to another surface which may be a horizontal or non-horizontal datum. 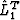 is the propagator corresponding to the topographic surface, and
is the propagator corresponding to the topographic surface, and 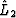 is the propagator to a horizontal datum. Now the Hessian matrix
is the propagator to a horizontal datum. Now the Hessian matrix 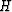 has a relation to the topography and the acquisition configuration. Similarly, if the Hessian matrix is an ideal full-pass filter, equation (
has a relation to the topography and the acquisition configuration. Similarly, if the Hessian matrix is an ideal full-pass filter, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be rewritten as
) can be rewritten as
| 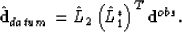 |
(8) |
However, if a suitable Hessian filter is chosen, the quality of data mapping will be improved further.
Next, we discuss data regularization with common-offset prestack time migration and the necessity of anti-aliasing for processing land data sets.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the estimated and regular data set can be found:
), the estimated and regular data set can be found:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the ideal wave propagator L is unknown, but it can be replaced with the practical wave propagator
), the ideal wave propagator L is unknown, but it can be replaced with the practical wave propagator ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be rewritten as
) can be rewritten as
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be rewritten as
) can be rewritten as
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The formula for redatuming should be modified as follows:
). The formula for redatuming should be modified as follows:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be rewritten as
) can be rewritten as