




Next: Real Data
Up: Sava and Biondi: Amplitude-preserved
Previous: Jacobian for Common-azimuth migration
The transformation Jacobians, given by Equation (23)
for reflection-angle gathers and by Equation (28)
for offset ray-parameter gathers, are strictly speaking
valid only for constant velocity media.
In the case of variable velocity, downward continuation is
implemented in the mixt 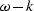 and
and  domain. The dispersion
relation is approximated using an expansion of the DSR equation.
In one of the most usual forms, the dispersion relation can be
written as
domain. The dispersion
relation is approximated using an expansion of the DSR equation.
In one of the most usual forms, the dispersion relation can be
written as
| 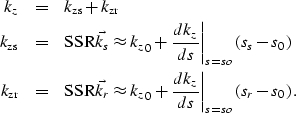 |
|
| |
| (39) |
Equations (39) give the effective dispersion
relation for which we need to implement the Jacobian weighting.
Appendix A outlines the derivation for the expresion of the
Jacobian in variable velocity media. For the case of migration
with output in offset, the Jacobian expression is:
| ![\begin{displaymath}
\bold W_k_h=
\left [
\frac{\omega s_0}{{k_{\rm zs_0}}} s_0+...
...{k_z}_0}\right ]^2 \right )\left (s_r-s_0\right )
\right ]^{-1}\end{displaymath}](img74.gif) |
(40) |
where 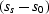 and
and 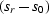 are respectively the slowness perturbations
at the source and receiver. In constant velocity media,
are respectively the slowness perturbations
at the source and receiver. In constant velocity media,
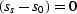 and
and 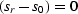 , Equation (40) obviously
takes the same form as Equation (23) we derived earlier
for the case of constant velocity.
, Equation (40) obviously
takes the same form as Equation (23) we derived earlier
for the case of constant velocity.
For the expressions of all Jacobians, we need to
compute the quantity 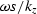 which may lead
to numerical instability when kz approaches zero.
A simple way so stabilize the Jacobian, which we have used for
the current examples, is to add a small positive quantity to
the denominator, and compute
which may lead
to numerical instability when kz approaches zero.
A simple way so stabilize the Jacobian, which we have used for
the current examples, is to add a small positive quantity to
the denominator, and compute 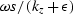 .
.
Another approach, which we have not tested yet,
but which appears to have the potential to be more accurate, is
to write
| ![\begin{eqnarray}
\frac{\omega s}{k_z}
&=&
\frac{\omega s}{{\rm SSR}{\vec{k}}} \...
...}{\sqrt{1-\frac{{\bf m}{\vec{k}}^2}{\left [2\omega s\right ]^2}}}.\end{eqnarray}](img81.gif) |
|
| (41) |
For small values of ![$x={\bf m}{\vec{k}} / \left [2\omega s\right ]$](img82.gif) we can
compute
we can
compute 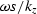 using the following Taylor series expansion:
using the following Taylor series expansion:
| 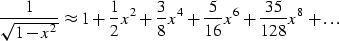 |
(42) |
This expansion is very similar to the transformation used by
Huang et al. (1999) for the extended Local Born Fourier migration
method, or by Sava and Biondi (2000) in wave-equation MVA.
This interesting possibility, however, awaits future research.





Next: Real Data
Up: Sava and Biondi: Amplitude-preserved
Previous: Jacobian for Common-azimuth migration
Stanford Exploration Project
4/30/2001
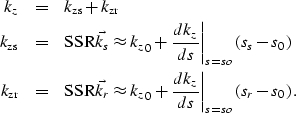
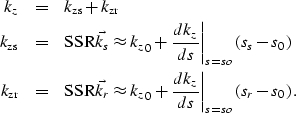
![\begin{displaymath}
\bold W_k_h=
\left [
\frac{\omega s_0}{{k_{\rm zs_0}}} s_0+...
...{k_z}_0}\right ]^2 \right )\left (s_r-s_0\right )
\right ]^{-1}\end{displaymath}](img74.gif)
![]() which may lead
to numerical instability when kz approaches zero.
A simple way so stabilize the Jacobian, which we have used for
the current examples, is to add a small positive quantity to
the denominator, and compute
which may lead
to numerical instability when kz approaches zero.
A simple way so stabilize the Jacobian, which we have used for
the current examples, is to add a small positive quantity to
the denominator, and compute ![]() .
.![\begin{eqnarray}
\frac{\omega s}{k_z}
&=&
\frac{\omega s}{{\rm SSR}{\vec{k}}} \...
...}{\sqrt{1-\frac{{\bf m}{\vec{k}}^2}{\left [2\omega s\right ]^2}}}.\end{eqnarray}](img81.gif)