




Next: Ray-parameter gathers
Up: Transformation Jacobians
Previous: Transformation Jacobians
For reflection-angle gathers, the dispersion relation used to
downward continue the wavefield is given by the DSR equation:
| 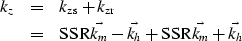 |
|
| (22) |
where s is the local slowness, 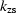 and
and 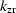 are respectively the vertical wavenumber for the source and receiver
components, and
are respectively the vertical wavenumber for the source and receiver
components, and 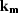 and
and 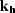 are respectively the midpoint and
offset wavenumbers.
ghmig
are respectively the midpoint and
offset wavenumbers.
ghmig
Figure 10 Reflection-angle gather implemented using
Equation (20). We do not use the correct weighting of
the transformation Jacobian, therefore the amplitudes are distorted.
 gpmig
gpmig
Figure 11 Offset ray-parameter gather implemented using
Equation (21). We do not use the correct weighting of
the transformation Jacobian, therefore the amplitudes are distorted.

The Jacobian for this transformation is thus the common
prestack Stolt migration Jacobian:
| ![\begin{eqnarray}
\bold W_k_h
&=& \left.\frac{d\omega}{dk_z}\right\vert _{{\bf {k...
...\rm zs}}} +
\frac{\omega s}{{k_{\rm zr}}} \right )
\right ]^{-1}.\end{eqnarray}](img47.gif) |
|
| (23) |
As mentioned in the preceding sections, in the case of variable
velocity media, those quantities are evaluated at the reflector location.
For an arbitrary 2-D reflector geometry (Figure 1),
we can rewrite Equation (23) as
| ![\begin{displaymath}
\bold W_k_h= \left [s\left (\frac{1}{\cos \left [\gamma-\alp...
...rac{1}{\cos \left [\gamma+\alpha\right ]}\right )\right ]^{-1},\end{displaymath}](img48.gif) |
(24) |
where  is the structural dip angle, and
is the structural dip angle, and 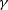 is the reflection
angle.
is the reflection
angle.
For flat reflectors, defined by 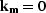 and
and 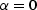 ,
the Jacobian takes the simple form
,
the Jacobian takes the simple form
| 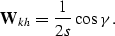 |
(25) |
chmig
Figure 12 Reflection-angle gather computed in the
image space. The weighting factors restore correct amplitudes.
Compare with the theoretical response in Figure 10.
 cpmig
cpmig
Figure 13 Offset ray-parameter gather computed in the
data space. The weighting factors restore correct amplitudes.






Next: Ray-parameter gathers
Up: Transformation Jacobians
Previous: Transformation Jacobians
Stanford Exploration Project
4/30/2001


![\begin{eqnarray}
\bold W_k_h
&=& \left.\frac{d\omega}{dk_z}\right\vert _{{\bf {k...
...\rm zs}}} +
\frac{\omega s}{{k_{\rm zr}}} \right )
\right ]^{-1}.\end{eqnarray}](img47.gif)
![\begin{displaymath}
\bold W_k_h= \left [s\left (\frac{1}{\cos \left [\gamma-\alp...
...rac{1}{\cos \left [\gamma+\alpha\right ]}\right )\right ]^{-1},\end{displaymath}](img48.gif)
![]() and
and ![]() ,
the Jacobian takes the simple form
,
the Jacobian takes the simple form

