Next: Variable-velocity Jacobians
Up: Sava and Biondi: Amplitude-preserved
Previous: Ray-parameter gathers
The dispersion relation of
3-D common-azimuth migration can be written as a cascade of
2-D inline prestack migration and
2-D zero-offset crossline migration Biondi (1999):
| 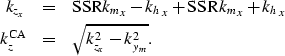 |
|
| (32) |
We can derive the expression for the common-azimuth
Jacobian by simply applying the chain rule to Equation (32):
| 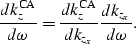 |
(33) |
If we note that
| 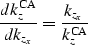 |
(34) |
we obtain the common-azimuth Jacobian:
| 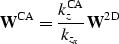 |
(35) |
where 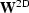 is the 2-D version of the Jacobian we derived in
the preceding sections, either for reflection-angle ADCIGs,
Equation (23), or for offset ray-parameter,
Equation (28).
is the 2-D version of the Jacobian we derived in
the preceding sections, either for reflection-angle ADCIGs,
Equation (23), or for offset ray-parameter,
Equation (28).
However, computing the reflection operator weight, Equation (2),
and the WKBJ amplitudes, Equation (11),
requires us to evaluate separately the source 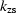 and
receiver
and
receiver 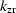 components of the dispersion relation.
Therefore, for the ``true-amplitude'' migration weights,
Equation (12),
we need to use the more complicated expression
for the common-azimuth dispersion relation
as introduced by Biondi and Palacharla (1996).
components of the dispersion relation.
Therefore, for the ``true-amplitude'' migration weights,
Equation (12),
we need to use the more complicated expression
for the common-azimuth dispersion relation
as introduced by Biondi and Palacharla (1996).
In addition to the amplitude terms we have discussed in the preceding
sections, ``true-amplitude''
common-azimuth migration requires an additional
correction that takes into account that its dispersion relation
is obtained by a stationary-phase approximation
of the full 3-D DSR equation.
We, therefore, need to augment the amplitude term in
Equation (9) by another factor, which results
from stationary-phase approximation theory Bleistein and Handelsman (1975):
| 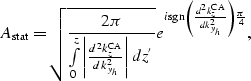 |
(36) |
where the second derivative of 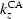 with respect to kyh is:
with respect to kyh is:
| ![\begin{eqnarray}
\frac{d^2k_z^{\rm CA}}{dk_{y_h}^2} =
&-&\frac{ \left (2\omega ...
...t )^2 - \left ({k_m}_y+\widehat{{k_h}_y}\right )^2 \right ]^{3/2}}\end{eqnarray}](img65.gif) |
|
| (37) |
with
| 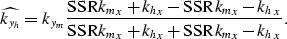 |
(38) |
This additional correction factor includes both a phase shift component
and an amplitude component which increases with depth.
It has thus a behavior similar to the correction
term that is often used to transform 2-D data recorded with
point sources and receivers to 2-D data recorded with
line sources and receivers Clayton and Stolt (1981).
The physical explanation is also analogous:
Common-azimuth migration assumes that the data
were recorded for all values of the crossline offset (yh)
and then stacked along yh.
The inverse of 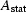 transforms the data recorded at zero crossline offset into
the data ``expected'' by common-azimuth migration.
transforms the data recorded at zero crossline offset into
the data ``expected'' by common-azimuth migration.
Figures 14-16
demonstrate the effects of applying the different weights in
common-azimuth migration.
These images are obtained by migrating a synthetic data set
containing five dipping reflectors with dips from 0 to 60 degrees
Biondi (2001).
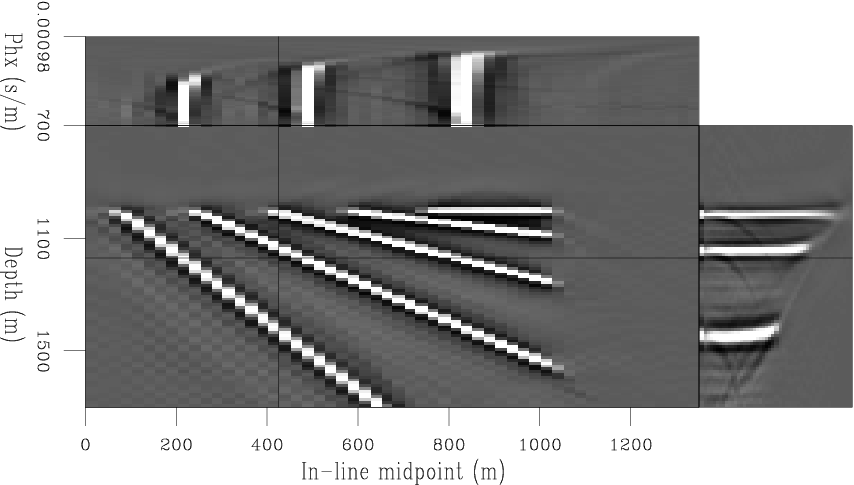
Figure 14
shows a subset of the migration results.
The front face of the cube displayed in the figure
is an in-line section stacked over ph.
The other two faces are sections through
the prestack image as a function of the offset ray
parameter (ph).
Those images are obtained by migration without any weighting factors.
Figure 15 shows the
same subset as in Figure 14,
but obtained by applying all
the appropriate weights and the phase shift related to the
stationary-phase approximation.
The weights balance the amplitudes along the reflector,
so that the dipping reflectors are comparable with the flat one.
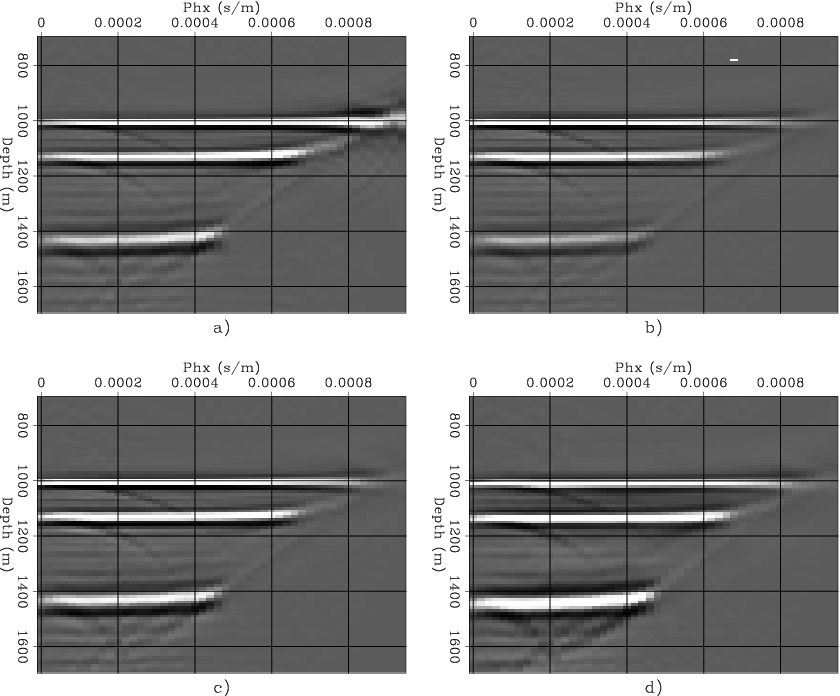
Figure 16 shows one particular ADCIG, detailing
the effects of each type of weighting:
no weights (Figure 16a),
Jacobian and modeling weights (Figure 16b),
Jacobian, modeling and WKBJ weights (Figure 16c), and
Jacobian, modeling, WKBJ and phase-shift weights (Figure 16d).
CA-pull-none-vp
Figure 14 A subset of the results of common-azimuth migration of the synthetic
data set.
The front face of the cube is an in-line section stacked along ph.
The other two faces are sections through the prestack image.
The migrated cube is obtained from migration without any weighting.
The amplitudes of the dipping reflectors are lower than expected,
and the whole image has the wrong phase.
 CA-pull-WKBJ-stat-vp
CA-pull-WKBJ-stat-vp
Figure 15 A subset of the results of common-azimuth migration of the synthetic
data set.
The front face of the cube is an in-line section stacked along ph.
The migrated cube is obtained from migration with
all the appropriate weights and the stationary-phase phase shift.
The amplitudes of the dipping reflectors are comparable with those of
the flat reflector,
and the whole image has the correct phase.
 CIG-amp
CIG-amp
Figure 16 ADCIGs obtained by common-azimuth migration with
different amplitude weights:
a) No weights,
b) 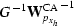 (Jacobian),
c)
(Jacobian),
c) 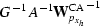 (Jacobian and WKBJ),
d)
(Jacobian and WKBJ),
d) 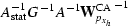 (Jacobian, WKBJ, and stationary phase).
The relative amplitudes of the dipping reflectors
are modified by the different migration weights.
(Jacobian, WKBJ, and stationary phase).
The relative amplitudes of the dipping reflectors
are modified by the different migration weights.






Next: Variable-velocity Jacobians
Up: Sava and Biondi: Amplitude-preserved
Previous: Ray-parameter gathers
Stanford Exploration Project
4/30/2001
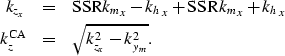
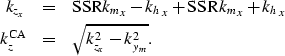
![]() and
receiver
and
receiver ![]() components of the dispersion relation.
Therefore, for the ``true-amplitude'' migration weights,
Equation (12),
we need to use the more complicated expression
for the common-azimuth dispersion relation
as introduced by Biondi and Palacharla (1996).
components of the dispersion relation.
Therefore, for the ``true-amplitude'' migration weights,
Equation (12),
we need to use the more complicated expression
for the common-azimuth dispersion relation
as introduced by Biondi and Palacharla (1996).
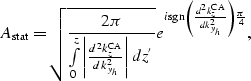
![\begin{eqnarray}
\frac{d^2k_z^{\rm CA}}{dk_{y_h}^2} =
&-&\frac{ \left (2\omega ...
...t )^2 - \left ({k_m}_y+\widehat{{k_h}_y}\right )^2 \right ]^{3/2}}\end{eqnarray}](img65.gif)
![]() transforms the data recorded at zero crossline offset into
the data ``expected'' by common-azimuth migration.
transforms the data recorded at zero crossline offset into
the data ``expected'' by common-azimuth migration.