




Next: Generalized screen
Up: Mixed-domain migration theory
Previous: Mixed-domain migration theory
In one of its most general forms Ristow and Ruhl (1994), we can write kz as
| ![\begin{displaymath}
k_z= {k_z}_o+ \omega\left[1- \frac{s}{s_o} \left(\sum\limits...
...hoose n} \S^{2n} \delta_n \right)\right]
\left(s - s_o\right),\end{displaymath}](img11.gif) |
(2) |
where 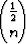 are binomial coefficients for integer
numbers n, s represents the spatially variable slowness function at depth z,
so is a constant approximation to s,
and
are binomial coefficients for integer
numbers n, s represents the spatially variable slowness function at depth z,
so is a constant approximation to s,
and 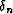 is a sum of terms derived from s and so.
The FFD equation is obtained using two Taylor series expansions of the SSR equations
written for kz and kzo.
I give a full derivation of Equation (2) in Appendix A.
is a sum of terms derived from s and so.
The FFD equation is obtained using two Taylor series expansions of the SSR equations
written for kz and kzo.
I give a full derivation of Equation (2) in Appendix A.
Higher accuracy can be achieved by replacing the Taylor expansion in
Equation (2) with Muir's continuous fraction expansion
Claerbout (1985). The equivalent form of the general Fourier
finite-difference propagator is:
| ![\begin{displaymath}
k_z= {k_z}_o+ \omega\left[1- \frac{s}{s_o} \left(\sum\limits...
...\frac{\S^2}{a_n+b_n \S^2} \right)\right]
\left(s - s_o\right),\end{displaymath}](img14.gif) |
(3) |
where an and bn are coefficients that, in general, depend on the medium
and the constant reference slownesses, s and so. The coefficients
an and bn are derived either by identification of terms between Equation (2) and
Equation (3), after the approximation 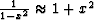 , or
by an optimization problem as described by Ristow and Ruhl (1997).
, or
by an optimization problem as described by Ristow and Ruhl (1997).





Next: Generalized screen
Up: Mixed-domain migration theory
Previous: Mixed-domain migration theory
Stanford Exploration Project
9/5/2000
![\begin{displaymath}
k_z= {k_z}_o+ \omega\left[1- \frac{s}{s_o} \left(\sum\limits...
...\frac{\S^2}{a_n+b_n \S^2} \right)\right]
\left(s - s_o\right),\end{displaymath}](img14.gif)