




Next: Fourier finite-difference
Up: Sava: Mixed-domain operators
Previous: Introduction
Downward continuation is the process in which we recursively extrapolate in depth
the wavefield recorded at the surface. Mathematically, this operation amounts to a
phase shift applied to the wavefield Claerbout (1985)

where Uz is the wavefield at depth z, and  is the extrapolated wavefield
at depth
is the extrapolated wavefield
at depth 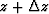 . The downward continuation operator at depth z is
. The downward continuation operator at depth z is
|  |
(1) |
with the vertical wavenumber, kz, given by the one-way wave equation,
also known as the single square root (SSR) equation

where  is the temporal frequency, s is the laterally variable slowness of
the medium, and
is the temporal frequency, s is the laterally variable slowness of
the medium, and  is the horizontal wavenumber.
is the horizontal wavenumber.
Since downward continuation by phase shift can be applied for slowness models
that only vary with depth, we need to split the operator 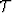 into two parts:
a constant slowness continuation operator applied in the
into two parts:
a constant slowness continuation operator applied in the 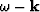 domain,
which accounts for the propagation in depth,
and a screen operator applied in the
domain,
which accounts for the propagation in depth,
and a screen operator applied in the 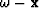 domain,
which accounts for the wavefield perturbations due to the lateral slowness variations.
In essence, we approximate the vertical wavenumber kz with its constant
slowness counterpart kzo, corrected by a term describing the spatial
variability of the slowness function (Figure
domain,
which accounts for the wavefield perturbations due to the lateral slowness variations.
In essence, we approximate the vertical wavenumber kz with its constant
slowness counterpart kzo, corrected by a term describing the spatial
variability of the slowness function (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
screen
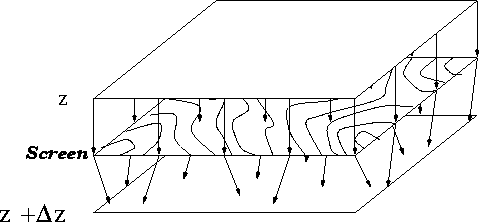
Figure 1 A sketch of mixed-domain migration. The wavefield at depth
z is downward continued to depth 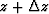 trough a variable-slowness screen. trough a variable-slowness screen.
|
|  |






Next: Fourier finite-difference
Up: Sava: Mixed-domain operators
Previous: Introduction
Stanford Exploration Project
9/5/2000
![]()
![]()
![]() into two parts:
a constant slowness continuation operator applied in the
into two parts:
a constant slowness continuation operator applied in the ![]() domain,
which accounts for the propagation in depth,
and a screen operator applied in the
domain,
which accounts for the propagation in depth,
and a screen operator applied in the ![]() domain,
which accounts for the wavefield perturbations due to the lateral slowness variations.
In essence, we approximate the vertical wavenumber kz with its constant
slowness counterpart kzo, corrected by a term describing the spatial
variability of the slowness function (Figure
domain,
which accounts for the wavefield perturbations due to the lateral slowness variations.
In essence, we approximate the vertical wavenumber kz with its constant
slowness counterpart kzo, corrected by a term describing the spatial
variability of the slowness function (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
