![\begin{displaymath}
k_z= {k_z}_o+ {k_z}_o\sum\limits_{n=1}^{\infty} \left(-1 \ri...
...rt^2} \right)\left(\frac{s_o^2-s^2}{s_o^2} \right)
\right]
}^n.\end{displaymath}](img16.gif)
![\begin{displaymath}
k_z= {k_z}_o+ {k_z}_o\sum\limits_{n=1}^{\infty} \left(-1 \ri...
...rt^2} \right)\left(\frac{s_o^2-s^2}{s_o^2} \right)
\right]
}^n.\end{displaymath}](img16.gif) |
(4) |
Equation (4) may become unstable when the denominator of the sum vanishes. One way to avoid such a situation is to replace the vanishing term with another Taylor series expansion
![\begin{displaymath}
k_z= {k_z}_o+ {k_z}_o\sum\limits_{n=1}^{\infty} \left(-1 \ri...
...t]}^i \right)\left(\frac{s_o^2-s^2}{s_o^2} \right)
\right]
}^n.\end{displaymath}](img17.gif) |
(5) |
We can use Equations (2) and (5) to derive the formulae for many of the methods commonly referred to as screen propagators, using various approximations for the vertical wavenumber kz. For simplicity, however, in the next sections I use the Fourier finite-difference equation (2), because it offers a much more straight-forward derivation of the simplified cases, together with easier implementation. Nevertheless, Equation (5) can also be used to obtain the simplified cases, as presented in Appendix B.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is a comparison of the angular accuracy achieved by the
two methods, FFD and GSP. GSP achieves higher angular accuracy compared to FFD
for the same order of the approximation, although, as mentioned earlier, stability
requires further approximations that inevitably decrease the accuracy of GSP.
Furthermore, the GSP equation involves kzo in the Taylor series expansion,
which does not have a straightforward finite-difference implementation.
is a comparison of the angular accuracy achieved by the
two methods, FFD and GSP. GSP achieves higher angular accuracy compared to FFD
for the same order of the approximation, although, as mentioned earlier, stability
requires further approximations that inevitably decrease the accuracy of GSP.
Furthermore, the GSP equation involves kzo in the Taylor series expansion,
which does not have a straightforward finite-difference implementation.
|
ffdgsp
Figure 2 Angular accuracy comparison between FFD and GSP. The horizontal axis is the propagation angle, while the vertical axis is the ratio of the approximate and true values of the depth wavenumbers. Various curves correspond to different levels of accuracy. The thicker line corresponds to the split-step Fourier method. The dashed line corresponds to FFD using a second order Muir continuous fraction expansion. For both FFD and GSP, the higher order approximations achieve higher accuracy. The graphs correspond to 1/s=2.0 km/s and 1/so=1.9 km/s. | 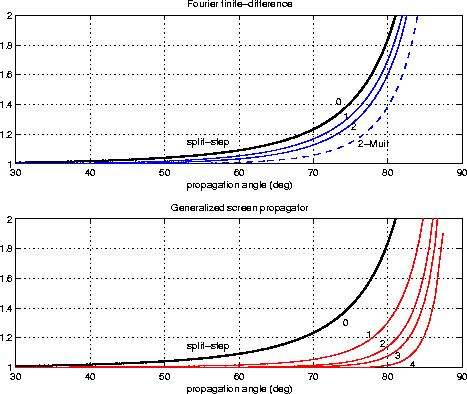 |