REFERENCES

Biondi, B., and Sava, P., 1999, Wave-equation migration velocity analysis: SEP-100, 11-34.

Biondi, B. L., 1999, 3-D Seismic Imaging: Stanford Exploration Project.

Claerbout, J. F., 1985, Imaging the Earth's Interior: Blackwell Scientific Publications.

Clapp, R. G., and Biondi, B., 1999, Preconditioning tau tomography with geologic constraints: SEP-100, 35-50.

de Hoop, M. V., and Wu, R. S., 1996, General formulation of screen methods for the scattering of waves in inhomogeneous media: Wave Motion, submitted.

de Hoop, M. V., 1996, Generalization of the Bremmer coupling series: J. Math. Phys., 3246-3282.

Gazdag, J., and Sguazzero, P., 1984, Migration of seismic data by phase-shift plus interpolation: Geophysics, 49, no. 2, 124-131.

Gazdag, J., 1978, Wave equation migration with the phase-shift method: Geophysics, 43, no. 7, 1342-1351.

Huang, L.-J., and Wu, R.-S., 1996, 3-D prestack depth migration with acoustic pseudo-screen propagators in Hassanzadeh, S., Ed., Mathematical methods in geophysical imaging IV:: Proc. SPIE: The International Society for Optical Engineering, 40-51.

Huang, L., Fehler, M. C., and Wu, R. S., 1999, Extended local Born Fourier migration method: Geophysics, 64, no. 5, 1524-1534.

Le Rousseau, J., and de Hoop, M., 1998, Modeling and imaging with the generalized screen algorithm: 68th Ann. Internat. Meeting, Soc. Expl. Geophys., 1937-1940.

Prucha, M. L., Biondi, B. L., and Symes, W. W., 1999, Angle-domain common image gathers by wave-equation migration: SEP-100, 101-112.

Ristow, D., and Ruhl, T., 1994, Fourier finite-difference migration: Geophysics, 59, no. 12, 1882-1893.

Ristow, D., and Ruhl, T., 1997, 3-D implicit finite-difference migration by multiway splitting: Geophysics, 62, no. 02, 554-567.

Sava, P., and Biondi, B., 2000, Wave-equation migration velocity analysis: Episode II: SEP-103, 19-47.

Sava, P., and Fomel, S., 2000, Angle-gathers by Fourier Transform: SEP-103, 119-130.

Sava, P., 2000, Variable-velocity prestack Stolt residual migration with application to a North Sea dataset: SEP-103, 147-157.

Stoffa, P. L., Fokkema, J. T., de Luna Freire, R. M., and Kessinger, W. P., 1990, Split-step Fourier migration: Geophysics, 55, no. 4, 410-421.

Vaillant, L., and Sava, P., 1999, Common-azimuth migration of a North Sea dataset: SEP-102, 1-14.

A This Appendix is a step-by-step derivation of the Fourier finite-difference equation, Equation (2), one of the most general forms of the equations describing mixed-domain migration.

I begin with Taylor series approximations of the single square root equations for the vertical wavenumbers corresponding to the true slowness (s)  

$$k_z= \sqrt{\omega^2 { s }^2 - \left\vert \bf k_m\right\vert^... ...ight)^n \displaystyle{\frac{1}{2} \choose n} \S^{2n} \right] ,$$ (18)

and for the reference slowness (s_o)  

$${k_z}_o= \sqrt{\omega^2 {s_o}^2 - \left\vert \bf k_m\right\v... ...\left\vert \bf k_m\right\vert}{\omega s_o}\right]^{2n} \right],$$ (19)

where $${m \choose n}$$ are binomial coefficients for real m and integer n. We can use Equation (19) to replace k_zo in Equation (18) and obtain an equation relating the true depth wavenumber k_z to the reference one:

$$k_z= {k_z}_o+ \omega\left(s - s_o\right) + \omega\sum\limit... ...left\vert \bf k_m\right\vert}{\omega s_o}\right]^{2n} \right].$$ (20)

Next we re-arrange the slowness terms of the equation to facilitate the substitution of the ratio of the true and reference slownesses: $p = \frac{s}{s_o}$

$$k_z= {k_z}_o+ \omega s_o\left(\frac{s}{s_o} - 1\right) + \o... ... \S^{2n} \left[\frac{s}{s_o} - \frac{s^{2n}}{s_o^{2n}}\right],$$ (21)

which leads to the more compact relation:

$$k_z= {k_z}_o+ \omega s_o\left(p - 1\right) + \omega s_o\sum... ...ystyle{\frac{1}{2} \choose n} \S^{2n} \left[p - p^{2n} \right].$$ (22)

If we make the change of variables

$$\delta_n = \sum\limits_{l=0 \choose n\ge 1}^{2n-2} p^l,$$ (23)

we can write that

$$k_z= {k_z}_o+ \omega s_o\left(p - 1\right) - \omega s_o\lef... ...ght)^n \displaystyle{\frac{1}{2} \choose n} \S^{2n} \delta_n.$$ (24)

Next, if we add and subtract $\omega s_op \left(p - 1\right)$ on the right hand side of the preceding equation, we obtain that

$$k_z= {k_z}_o+ \omega s_o\left(p - 1\right)+ \omega s_op \lef... ...ight)^n \displaystyle{\frac{1}{2} \choose n} \S^{2n} \delta_n$$ (25)

which can be simplified to

$$k_z= {k_z}_o+ \omega s_o\left(p - 1\right)\left(p + 1\right)... ...ght)^n \displaystyle{\frac{1}{2} \choose n} \S^{2n} \delta_n,$$ (26)

and, furthermore, to

$$k_z= {k_z}_o+ \omega s_o\left(p - 1\right) \left[1+ p \left... ...ystyle{\frac{1}{2} \choose n} \S^{2n} \delta_n \right)\right],$$ (27)

and, finally, to

$$k_z= {k_z}_o+ \omega s_o\left(p - 1\right) \left[1- p \left... ...ystyle{\frac{1}{2} \choose n} \S^{2n} \delta_n \right)\right].$$ (28)

If we make the reverse change of variables from p to s and s_o, we obtain the general Taylor expansion form of the depth wavenumber used for the FFD migration method:  

$$k_z= {k_z}_o+ \omega\left[1- \frac{s}{s_o} \left(\sum\limits... ...hoose n} \S^{2n} \delta_n \right)\right] \left(s - s_o\right).$$ (29)

The equivalent 2^nd order equation takes the form:

$$k_z\approx {k_z}_o+ \omega\left[1 + \frac{1}{2} \frac{1}{s... ...t \bf k_m\right\vert^4}{\omega^4} \right]\left(s - s_o\right).$$

We can write an analogous form for Equation (29) using a continuous fraction expansion

$$k_z= {k_z}_o+ \omega\left[1- \frac{s}{s_o} \left(\sum\limits... ...\frac{\S^2}{a_n+b_n \S^2} \right)\right] \left(s - s_o\right).$$ (30)

The equivalent 2^nd order equation takes the form:

$$k_z\approx {k_z}_o+ \omega\left[1 - \frac { \frac{1}{s s_o... ...\bf k_m\right\vert^2}{\omega^2} } \right]\left(s - s_o\right).$$

B This appendix is a step-by-step derivation of the generalized screen equation.

I begin with the single square root equation for the true slowness (s)

$$k_z= \sqrt{\omega^2 {s}^2 - \left\vert \bf k_m\right\vert^2},$$

and for the background slowness (s_o)

$${k_z}_o= \sqrt{\omega^2 {s_o}^2 - \left\vert \bf k_m\right\vert^2}.$$

We can replace k_zo in k_z to get

$$k_z= \sqrt{{k_z}_o^2 - \omega^2 \left(s_o^2-s^2\right)},$$ (31)

or, in an equivalent form,

$$k_z= {k_z}_o\sqrt{1 - \frac{\omega^2 \left(s_o^2-s^2\right)}{{k_z}_o^2} }.$$

Next, we can write a Taylor series expansion, assuming a small slowness squared perturbation s²-s_o²

$$k_z= {k_z}_o\sum\limits_{n=0}^{\infty} \left(-1 \right)^n \... ...t[\frac{\omega^2\left(s_o^2-s^2\right)}{{k_z}_o^2} \right] }^n.$$

The 2^nd order approximation takes the form:

$$k_z= {k_z}_o -\frac{1}{2} \left[\frac{\omega^2}{{k_z}_o} \ri... ...t[\frac{\omega^2}{{k_z}_o} \right]^2 \left(s_o^2-s^2 \right)^2.$$

We can make k_zo explicit for the terms of the sum and obtain

$$k_z= {k_z}_o\sum\limits_{n=0}^{\infty} \left(-1 \right)^n \... ...rt^2} \right)\left(\frac{s_o^2-s^2}{s_o^2} \right) \right] }^n,$$ (32)

from which we can derive the generalized screen migration equation:  

$$k_z= {k_z}_o+ {k_z}_o\sum\limits_{n=1}^{\infty} \left(-1 \ri... ...rt^2} \right)\left(\frac{s_o^2-s^2}{s_o^2} \right) \right] }^n.$$ (33)

Because Equation (33) becomes unstable when the denominator of the terms in the summation vanishes, we replace these terms with another Taylor series expansion:  

$$k_z= {k_z}_o+ {k_z}_o\sum\limits_{n=1}^{\infty} \left(-1 \ri... ...t]}^i \right)\left(\frac{s_o^2-s^2}{s_o^2} \right) \right] }^n.$$ (34)

We can obtain the split-step equation through a sequence of approximations in Equation (34): first, we limit the terms of the inner Taylor series to two (i=1,2) and the terms of the outer series to one (n=1), therefore

$$k_z\approx {k_z}_o+ {k_z}_o\frac{-1}{2} \frac{\left(\omega s_o\right)^2}{{k_z}_o^2} \left(1-\frac{s^2}{s_o^2} \right),$$

which we can simplify to

$$k_z\approx {k_z}_o- \frac{1}{2} \frac{\omega^2}{{k_z}_o} \left(s_o^2 - s^2 \right).$$

Next, we approximate 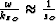$\frac{\omega}{{k_z}_o}\approx \frac{1}{s_o}$ and $s_o+s\approx2s_o$, and get

$$k_z\approx {k_z}_o- \frac{1}{2s_o} 2s_o\omega\left(s_o- s \right).$$

which reduces to the split-step equation

$$k_z\approx {k_z}_o+ \omega\left(s - s_o\right).$$