Examples with several wave-equation migration algorithms

Biondi and Vaillant 2000 discuss the relative accuracy of offset plane-wave migration and CAM for wave-equation imaging. Both are derived from full downward continuation of 3-D prestack data with the Double Square Root (DSR) phase-shift operator:

$$\begin{eqnarray} k_z & = & \sqrt{\frac{\omega^2}{v^2(\bold{s},z)} - \frac{1}{4} ... ...{mx} + k_{hx}\right)^2 + \left( k_{my} + k_{hy}\right)^2 \right]}\end{eqnarray}$$ (10)

where $\omega$ is the temporal frequency, $\bold{k_m}$ is the midpoint wavenumber vector, $\bold{k_h}$ is the offset wavenumber vector, $v(\bold{g},z)$ and $v(\bold{g},z)$ are the velocity at the source and receiver locations, respectively.

Offset plane wave (OPW) migration Mosher et al. (1997) performs migration of each offset plane wave component of the data independently. It can be interpreted as a reversed-order two-pass prestack migration, where an initial cross-line zero-offset migration is followed by an in-line prestack migration. Another interpretation in that the cross-line offset wavenumber k_hy in equation (10) is set to zero for downward continuation:

$$\begin{eqnarray} k_z & = & \sqrt{\frac{\omega^2}{v^2(\bold{s},z)} - \frac{1}{4} ... ...1}{4} \left[ \left( k_{mx} + k_{hx}\right)^2 + k_{my}^2 \right]}\end{eqnarray}$$ (11)

Instead, for CAM, the cross-line offset wavenumber k_hy is replaced in equation (10) by its stationary path $\hat{k}_{hy}$ given in equation (9):

$$\begin{eqnarray} k_z & = & \sqrt{\frac{\omega^2}{v^2(\bold{s},z)} - \frac{1}{4} ... ...+ k_{hx}\right)^2 + \left( k_{my} + \hat k_{hy}\right)^2 \right]}\end{eqnarray}$$ (12)

Both migrations reduce the full 5-D phase-shift operator to a 4-D operator. In fact, when no multipathing occurs, only a 4-D slice of the 5-D wavefield contributes to the image.

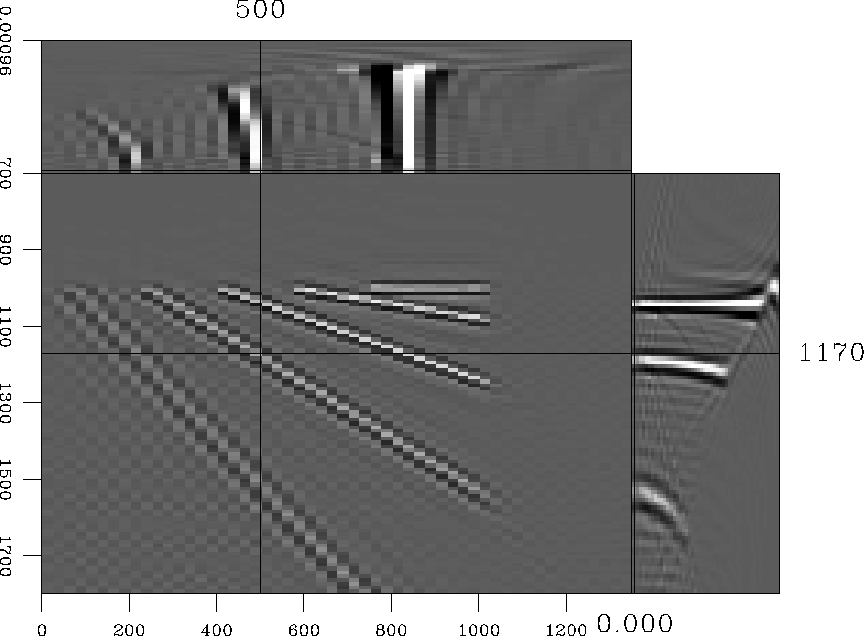
Figures 9 and 10 show migration results. The final image cube has 4 dimensions, the last being the common-image gather (CIG) ray parameter axis, generated by slant stack Prucha et al. (1999). The CIGs are flat for the first reflectors (dips $0-30^\circ$) in both images. For OPW migration, non-flat gathers start at dip $45^\circ$, whereas only a dip of $60^\circ$ causes trouble to CAM.

 

CA-mig-sect1
Figure 9 3-D cube extracted from the 4-D image cube migrated with CAM, at location cmp-y=500m. Central panel (cmp-x / depth) shows all 5 dipping planes. Ray parameter domain CIGs show flat gathers except for the reflector dipping at $60^\circ$.

 

OPW-mig-sect1
Figure 10 3-D cube extracted from the 4-D image cube migrated with Offset-plane waves migration, at location cmp-y=500m. Ray parameter domain CIGs show perturbed gathers for reflectors dipping at $45^\circ$and $60^\circ$.

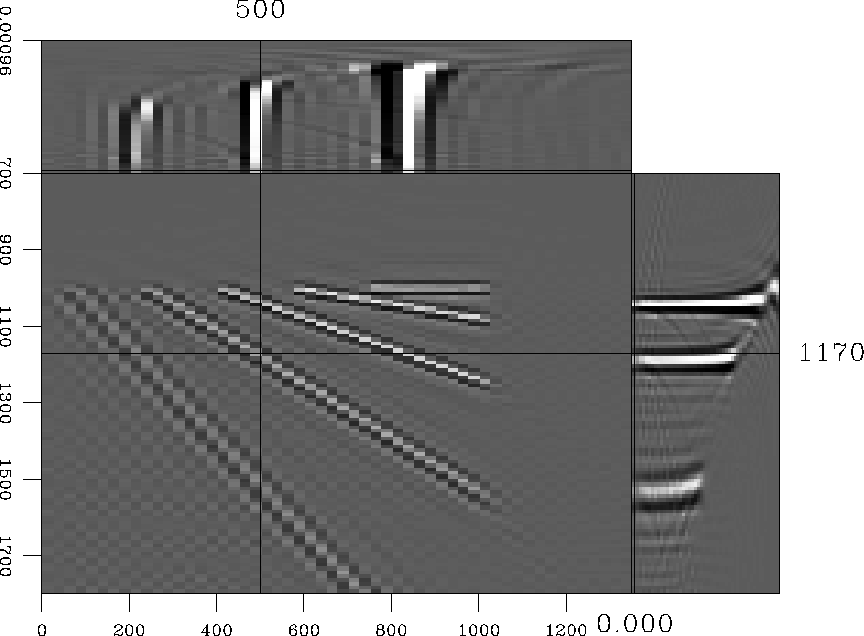
In order to have a reference for comparison, we migrated the 4-D common-azimuth data with 5-D phase-shift migration, after zero-padding along a fictitious cross-line offset axis (Figure 8). Figure 11 shows flat gathers even for the most strongly dipping reflectors.

For using the full 5-D phase-shift operator, we added a fictitious cross-line offset axis by zero-padding common-azimuth data. The ``arbitrary'' parameters n_hy and d_hy are chosen in order to avoid wraparound problems in Fourier Transforms (n_hy large enough) and to have the exact value of k_hy included in our k_hy range. In practice, we used n_hy=24 and d_hy=50m.

 

PS-mig-sect1
Figure 11 3-D cube extracted from the 4-D image cube migrated with a 5-D phase-shift operator, at location cmp-y=500m. Ray parameter domain CIGs show completely flat gathers even at steep dips, as expected.