The road to Narrow-Azimuth Migration (NAM)

Vaillant and Biondi 1999 reviewed common-azimuth migration theory and examined how to extend the method to a ``narrow'' range of azimuths. The previous discussion illustrates opportunities for obtaining the accuracy of the full 5-D phase-shift operator at a lower cost. Effectively, most of the contributions to the final image are concentrated in a cross-line offset wavenumber k_hy centered around CAM stationary path $\hat{k}_{hy}$. Summing all contributions coherently in such a narrow range (see Figure 12) can reduce the cost of applying the full 5-D phase-shift operator by a factor of about 5, with potentially the same accuracy at all dips.

 

phy_nam Figure 12 Same reflector as in Figure 6. The dashed curve represents the stationary path 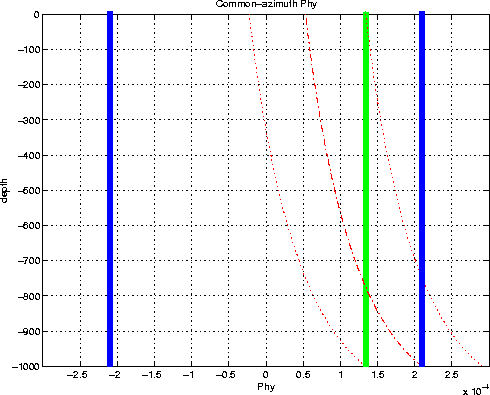$\hat{k}_{hy}$, with the estimated range needed for narrow-azimuth migration on the sides (dotted curves). The solid grey line is the exact value of khy. Black solid lines represent the minimum range needed for the full 5-D phase-shift operator.