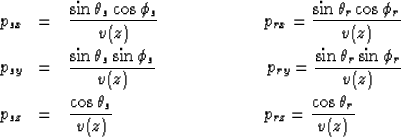
In the cartesian coordinate system, the components of the source and receiver slowness vectors along a ray are
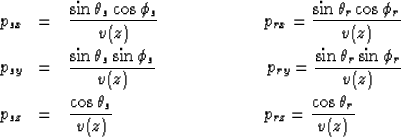 |
(6) | |
| (7) | ||
| (8) |
In this context, we can reformulate the expression for the stationary path in CAM theory Biondi and Palacharla (1996), which gives the cross-line offset ray parameter as a function of velocity and ray parameters:
| |
(9) |
Moreover, since wave propagation can be handled completely
analytically in constant gradient velocity, we can calculate the
theoretically ``exact'' cross-line offset wavenumber and compare it to
the values given by the stationary-phase approximation
(Equation (9)), as shown in
Figure 6. Here, in the case of a reflection on a plane
dipping at ![]() and oriented at
and oriented at ![]() with respect to the
in-line direction, the stationary path given by
Equation (9) is a seriously biased approximation.
with respect to the
in-line direction, the stationary path given by
Equation (9) is a seriously biased approximation.
|
phy_cam
Figure 6 Comparison of the exact cross-line offset ray parameter phy (thick solid line) and of the approximated phy (dashed curve) calculated with CAM stationary-phase approximation, in the case of a reflector dipping at about | 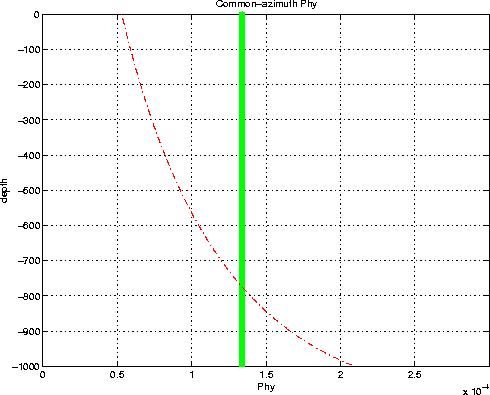 |