Analytical ray tracing

Theory shows that even in a simple 1-D v(z) medium, CAM is not perfectly accurate: the stationary-phase approximation used in the derivation of CAM Biondi and Palacharla (1996) imposes the relation among ray parameters indicated below that constrains rays to keep the same azimuth at each depth step (Figure 1):  

$$\frac{p_{sy}}{p_{sz}} = \frac{p_{ry}}{p_{rz}},$$ (1)

where the subscripts s and r refer to the rays coming from the source and the receiver, respectively.

 

ray-comaz Figure 1 Ray geometry imposed by common-azimuth constraints: both receiver and source rays keep the same azimuth at each depth step.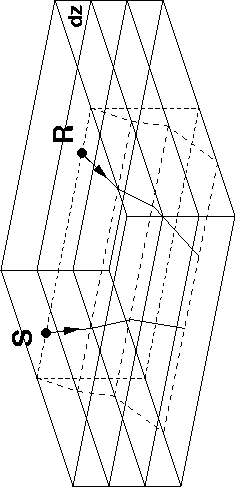

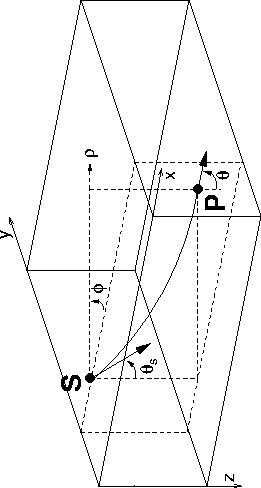
We choose to test the behavior of rays and the accuracy of CAM approximations in a synthetic medium where the velocity varies linearly. In such a medium, ray trajectories can be computed analytically, as well as all ray parameters. Figure 2 illustrates the geometry of the problem. With those notations, ray curvature can be expressed as Aki and Richards (1980):

$$\kappa = \frac{\vert\vert \nabla \bold{v} \vert\vert}{v} \sin \theta$$ (2)

In constant gradient velocity media where $v(z)=v_0+\gamma z$, the ray curvature is thus constant, i.e., rays are portions of circles included in a vertical plane. The radius of those circles is

$$R = \frac{1}{\kappa} = \frac{v(z)}{\gamma \sin \theta(z)} = \frac{v_0}{\gamma \sin \theta_s}$$ (3)

 

ray-vgrad
Figure 2 Ray geometry in a constant gradient velocity medium.

The ratio $\frac{\sin \theta(z)}{v(z)}$ is also the horizontal component $p_\rho$ of the slowness vector along the ray, which therefore is also a constant:

$$R = \frac{1}{\kappa} = \frac{1}{\gamma p_\rho} = \mbox{cst}$$ (4)

After some calculation (see Appendix), the equation of the circle of radius R passing through point source $S(\rho_s,z_s)$ with initial incident angle $\theta_s$ is, in the plane $(S,\rho,z)$: 

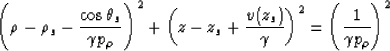$$\left( \rho - \rho_s - \frac{\cos \theta_s}{\gamma p_\rho} \... ...}{\gamma} \right)^2 = \left( \frac{1}{\gamma p_\rho} \right)^2$$ (5)

For any given triplet of points (S,P,R), respectively source, image point and receiver locations, there exist only two circles satisfying equation (5) that form the complete ray path. Figures 3 to 5 illustrate such ray paths. We can verify that the projections of the source ray and the receiver ray on the cross-line plane do not coincide in general and therefore break the assumption of azimuth conservation in CAM downward-continuation imposed by relation (1).

 

ray_exmpl1 Figure 3 Example of 3-D analytical ray tracing, with the three projections of both rays on vertical and horizontal planes. Source and receiver location are indicated with solid stars. The reflection point and its three projections are represented by a circle. Offset is 3000m (in-line). Velocity is 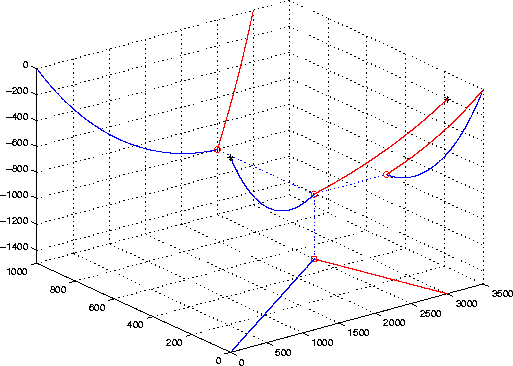$v(z)=1500+0.5z\;\mbox{m/s}$.

 

ray_exmpl2 Figure 4 Same geometry as before. The only difference is in the velocity: $v(z)=1500+z\;\mbox{m/s}$. The source ray has overturned because of the stronger velocity gradient.

 

ray_exmpl3 Figure 5 Velocity law is 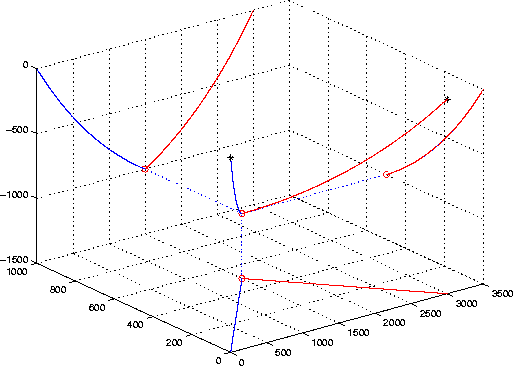$v(z)=1500+0.5z\;\mbox{m/s}$. The reflection point is at an equal distance from source and receiver: the problem is symmetrical and azimuth is conserved at each depth step.

However, with too strong a velocity gradient, rays quickly start to overturn (Figure 4). The corresponding reflection cannot be imaged with one-way wave propagation methods, such as CAM and the other wave-equation migration methods we discuss in this paper.