




Next: Comparing constant-velocity migration operators
Up: Efficient wave-equation migrations of
Previous: Common-azimuth downward continuation
Offset plane wave migration reduces
the computational complexity of downward continuation
of common-azimuth data
one step further than common-azimuth migration does.
It approximates the application of the full 5-D operator
expressed in equation (2)
with the application of several 3-D downward continuation
operators.
These 3-D operators are applied to common-azimuth data
after plane-wave decomposition along the offset axis.
The first step of the method is thus the decomposition
of the common-azimuth data into offset plane waves.
Each plane wave is then independently
downward continued.
Full downward continuation of offset plane waves could be
performed by applying
following operator
| 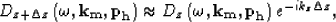 |
(6) |
where the vertical wavenumber kz is
now function of the offset plane wave parameters
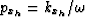 and
and
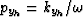 ;that is,
;that is,
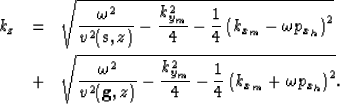
| ![\begin{eqnarray}
k_z& = &
\sqrt{
\frac{\omega^2}{v^2({{\bf s},z})} -
\frac{1}{...
...{x_h}\right)^2 + \left(k_{y_m}+\omega p_{y_h}\right)^2 \right]}
.\end{eqnarray}](img15.gif) |
|
| (7) |
Strictly speaking,
only in vertically layered media
can each plane wave be downward continued independently.
The plane waves should be allowed to mix at each depth step
when lateral velocity variations occur.
Therefore, the computationally attractive
feature of imaging each plane wave independently
also causes limitations in accuracy.
These limitations are difficult to study analytically,
and thus in a following section
I will analyze their effects
by comparing migration results below a complex
overburden (eg. a salt body).
In practice,
because common-azimuth data has
no cross-line offset axis,
the plane wave decomposition is performed only as a function
of the in-line offset ray parameter pxh,
and the cross-line offset ray parameter pyh is
assumed to be zero.
This assumption introduces another approximation
in the migration operator,
that can be studied analytically.
When pyh is set to zero,
equation (7)
becomes:
|  |
|
| (8) |
This equation is equivalent to the offset plane wave equation
presented by Mosher et al. 1997.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
It is easy to verify that if we assume
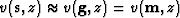 ,the dispersion relation of equation (8)
can be expressed as the cascade of
a zero-offset downward continuation along the cross-line
direction:
,the dispersion relation of equation (8)
can be expressed as the cascade of
a zero-offset downward continuation along the cross-line
direction:
| 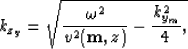 |
(9) |
and prestack downward continuation
along the in-line direction:
| 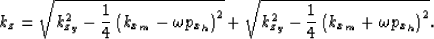 |
(10) |
The interpretation of this decomposition
is similar to the one discussed above for common-azimuth migration.
A constant velocity offset plane wave migration
that uses the dispersion relation of equation (8)
is equivalent to a constant-velocity cross-line zero-offset migration,
followed by a constant-velocity in-line prestack migration.
The order between these migrations
is thus reversed with respect to the correct order.
We analyze the implications of this
order reversal in the following section.





Next: Comparing constant-velocity migration operators
Up: Efficient wave-equation migrations of
Previous: Common-azimuth downward continuation
Stanford Exploration Project
10/25/1999
![\begin{eqnarray}
k_z& = &
\sqrt{
\frac{\omega^2}{v^2({{\bf s},z})} -
\frac{1}{...
...{x_h}\right)^2 + \left(k_{y_m}+\omega p_{y_h}\right)^2 \right]}
.\end{eqnarray}](img15.gif)

![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
![]() ,the dispersion relation of equation (8)
can be expressed as the cascade of
a zero-offset downward continuation along the cross-line
direction:
,the dispersion relation of equation (8)
can be expressed as the cascade of
a zero-offset downward continuation along the cross-line
direction: