




Next: Common-azimuth downward continuation
Up: Biondi: Offset plane waves
Previous: Introduction
The full downward continuation of 3-D prestack data
can be expressed in the frequency-wavenumber domain
by the following phase-shift operator
| 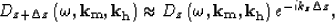 |
(1) |
where 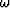 is the temporal frequency,
is the temporal frequency,
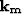 is the midpoint-wavenumber vector,
is the midpoint-wavenumber vector,
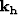 is the offset-wavenumber vector,
and
is the offset-wavenumber vector,
and 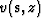 and
and 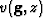 are respectively the velocity at the source
and receivers locations.
The vertical wavenumber kz is given
by the Double Square Root (DSR),
are respectively the velocity at the source
and receivers locations.
The vertical wavenumber kz is given
by the Double Square Root (DSR),
| ![\begin{eqnarray}
k_z& = &
\sqrt{
\frac{\omega^2}{v^2({{\bf s},z})} -
\frac{1}{...
...x_m}+k_{x_h}\right)^2 + \left(k_{y_m}+k_{y_h}\right)^2 \right]}
.\end{eqnarray}](img7.gif) |
|
| (2) |
This operator is a function of the cross-line component
of the offset wavenumber kyh,
while common-azimuth data are independent of kyh
because they are different from zero only at yh=0.
Therefore, the exact full downward continuation
is performed by applying a 5-D operator on
a data set that is only 4-D.
While accurate, this procedure is tremendously
wasteful of computational efforts,
because only a small subset of the 5-D wavefield contributes
to the final image.
The final image is formed
by extracting the zero-offset cube
from the downward-continued wavefield.
This data extraction is equivalent to the summation of the wavefield
along both offset-wavenumber axes.
Most of the wavefield components
destructively interfere in the imaging step.
In fact, only a 4-D slice of the 5-D wavefield contributes
to the image when no multipathing occurs,
such as in constant velocity or in a vertically layered media.
Even when multipathing occurs,
most of the wavefield components
destructively interfere in the imaging step.
It is therefore natural to limit
the computational cost by reducing the dimensionality of
the downward continuation operator from 5-D to 4-D.
Both common-azimuth migration and offset plane wave migration
achieve this goal, though in different ways.





Next: Common-azimuth downward continuation
Up: Biondi: Offset plane waves
Previous: Introduction
Stanford Exploration Project
10/25/1999
![\begin{eqnarray}
k_z& = &
\sqrt{
\frac{\omega^2}{v^2({{\bf s},z})} -
\frac{1}{...
...x_m}+k_{x_h}\right)^2 + \left(k_{y_m}+k_{y_h}\right)^2 \right]}
.\end{eqnarray}](img7.gif)