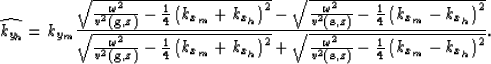
The analytical expression for kyh can be either obtained by geometric considerations or by a stationary-phase analysis, and is given as
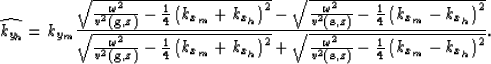 |
(3) |
The common-azimuth dispersion relation that is obtained by substituting equation (3) into equation (2) can be recast, after some algebraic manipulations, as a cascade of two dispersion relations. The first performs 2-D prestack downward-continuation along the in-line direction:
| |
(4) |
| |
(5) |
This rewriting of the common-azimuth dispersion connects common-azimuth migration to the theory of two-pass migration. In the special case of constant velocity, this connection is easily established through Stolt migration formalism Stolt (1978). Stolt migration is performed by stretching the temporal frequency (or the vertical wavenumber axis) according to the dispersion relation used for downward continuation. The cascade of two Stolt migrations is equivalent to a single Stolt migration that uses the cascade of the two dispersion relations.
In particular, common-azimuth Stolt migration is equivalent to in-line prestack Stolt migration followed by Stolt cross-line zero-offset migration. In the next section, we will show that this two-pass migration is also kinematically equivalent to the exact full-prestack migration of common-azimuth data.