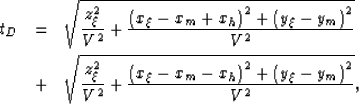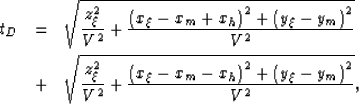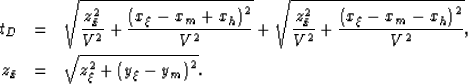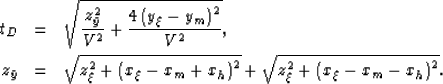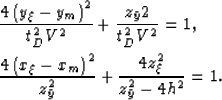Comparing constant-velocity migration operators

In constant velocity the summation surface of 3-D prestack migration is

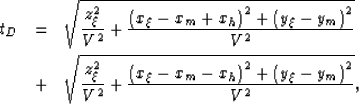$$\begin{eqnarray} t_{D}& = & \sqrt{\frac{z_\xi^2}{V^2}+\frac{\left(x_\xi-x_m+x_h\... ...frac{\left(x_\xi-x_m-x_h\right)^2+\left(y_\xi-y_m\right)^2}{V^2}},\end{eqnarray}$$ (11)

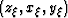where $(z_\xi,x_\xi,y_\xi)$ are the coordinates of the image point, (x_m,y_m) are the midpoint coordinates in data space, x_h is the in-line offset in data space, t_D is recording time in data space, and V is the medium velocity.

It is easy to verify that this summation surface is equivalent to the summation surface defined by the cascade of the two following expressions:

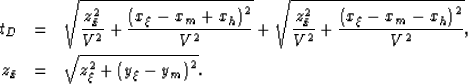$$\begin{eqnarray} t_{D}& = & \sqrt{\frac{z_{\bar x}^2}{V^2}+\frac{\left(x_\xi-x_m... ...{V^2}}, \\ z_{\bar x}& = &\sqrt{z_\xi^2+\left(y_\xi-y_m\right)^2}.\end{eqnarray}$$ (12) (13)

Equation (12) defines the summation path for 2-D prestack migration and corresponds to the dispersion relation in equation (4). Equation (13) defines the summation path for 2-D zero-offset migration and corresponds to the dispersion relation in equation (5). The straightforward interpretation of this result is that two-pass migration, in the correct order, is equivalent to full prestack migration, when the velocity is constant.

The dispersion relations of offset plane wave migration [equation (9) and equation (10)] respectively correspond to the following summation paths

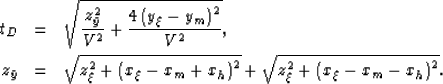$$\begin{eqnarray} t_{D}& = & \sqrt{\frac{z_{\bar y}^2}{V^2}+\frac{4\left(y_\xi-y_... ...i-x_m+x_h\right)^2} + \sqrt{z_\xi^2+\left(x_\xi-x_m-x_h\right)^2}.\end{eqnarray}$$ (14) (15)

The summation surface of offset plane wave migration is thus equivalent the cascade of these two paths. As noted before, the order of the two migration is reversed with respect to the correct one, and thus errors are introduced in the migration operator.

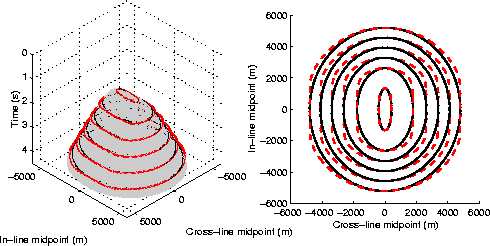
Figure 1 provides an intuitive understanding of the approximations involved in reversing the order of the migrations. The grey surface shown in the left panel of Figure 1 is the summation surface that should be used to image a diffractor at 500 m depth from data at a constant offset of 4,000 m, and assuming a constant velocity of 2,500 m/s. Two sets of contour lines are superimposed onto the surface. The inner set of contour lines corresponds to the exact summation surface, while the outer one corresponds to the surface defined by cascading the paths defined in equation (14) and equation (15). The right panel of Figure 1 shows the same contour lines in plane view. The solid lines correspond to the exact summation surface, while the dashed lines correspond to the approximate summation surface. Figure 1 graphically demonstrates that even in constant velocity, offset plane wave migration introduces an error for reflectors that are not exactly dipping in either the in-line direction or the cross-line direction.

 

planecheops
Figure 1 The grey surface shown in the left panel is the exact summation surface to image a diffractor at 500 m depth from data at a constant offset of 4,000 m, and assuming a constant velocity of 2,500 m/s. The solid contour lines correspond to the exact summation surface, while the dashed contour lines correspond to the approximate summation surface.

The analysis of the offset plane wave migration impulse response, or spreading surface, provides an alternative perspective to the analysis of the migration errors. The spreading surface of full 3-D prestack migration is the ellipsoid:

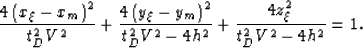$$\begin{eqnarray} & & { \frac{4\left(x_\xi-x_m\right)^2}{t_{D}^2V^2}+ \frac{4\lef... ...t)^2}{t_{D}^2V^2 - 4h^2}+ \frac{4z_\xi^2}{t_{D}^2V^2 - 4h^2}} = 1.\end{eqnarray}$$ (16)

It can be split as the cascade of the in-line prestack migration ellipse:

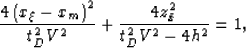$$\begin{eqnarray} & & { \frac{4\left(x_\xi-x_m\right)^2}{t_{D}^2V^2}+ \frac{4z_{\bar x}^2}{t_{D}^2V^2 - 4h^2}} = 1,\end{eqnarray}$$ (17)

and the cross-line zero-offset semicircle:

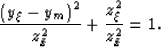$$\begin{eqnarray} & & { \frac{\left(y_\xi-y_m\right)^2}{z_{\bar x}^2}+ \frac{z_\xi^2}{z_{\bar x}^2}} = 1.\end{eqnarray}$$ (18)

The impulse response of offset plane wave migration, as defined by the dispersion relation in equation (8), is defined by the cascade of the following two impulse responses

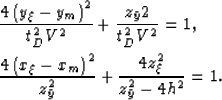$$\begin{eqnarray} & & { \frac{4\left(y_\xi-y_m\right)^2}{t_{D}^2V^2}+ \frac{z_{\b... ...ight)^2}{z_{\bar y}^2}+ \frac{4z_\xi^2}{z_{\bar y}^2 - 4h^2}} = 1.\end{eqnarray}$$ (19) (20)

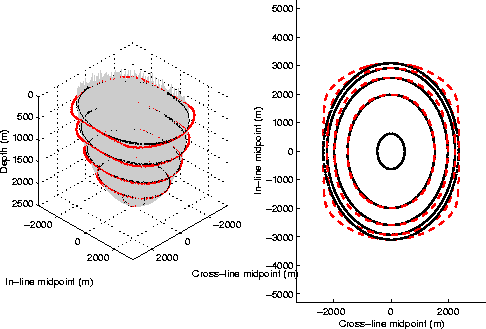
Figure 2 compares the exact impulse response of 3-D prestack migration and the offset plane wave approximation. The grey surface shown in the left panel of Figure 2 is the exact spreading surface for an impulse recorded at 2.5 s, at an offset of 4,000 m, and assuming a constant velocity of 2,500 m/s. The inner set of contour lines corresponds to the exact summation surface, while the outer one corresponds to the surface defined by cascading the paths defined in equation (19) and equation (20). The right panel of Figure 2 shows the same contour lines in plane view. The solid lines correspond to the exact spreading surface, while the dashed lines correspond to the approximate spreading surface. It is apparent that the approximation is worse for shallow reflectors dipping at 45 degrees with respect to the acquisition axes. This qualitative analysis is confirmed by the numerical results shown in the next section.

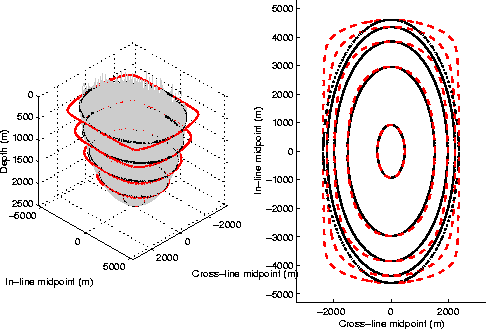
At zero offset the order of the in-line and cross-line migrations is obviously irrelevant; it is intuitive that the errors introduced by reversing the correct migration order increases with offset. To analyze the errors as a function of offset, Figure 3 compares the exact impulse response of 3-D prestack migration and the offset plane wave approximation at an offset of 8,000 m, and assuming the same constant velocity as in Figure 2 (2,500 m/s). The left panel of Figure 3 shows the exact spreading surface for an impulse recorded at 3.73 s. To make Figure 3 directly comparable with Figure 2, the impulse time was chosen to locate the bottom of the ellipsoid at exactly the same depth as in Figure 2, and the contour lines were drawn at the same depths as in Figure 2. It is apparent that at constant reflector depth the errors increase as the offset increases.

 

planeellips
Figure 2 The grey surface shown in the left panel is the exact spreading surface for an impulse at at 2.5 s, an offset of 4,000 m, and assuming a constant velocity of 2,500 m/s. The solid contour lines correspond to the exact spreading surface, while the dashed contour lines correspond to the approximate spreading surface.

 

planeellips8km
Figure 3 The grey surface shown in the left panel is the exact spreading surface for an impulse at at 3.73 s, an offset of 8,000 m, and assuming a constant velocity of 2,500 m/s. The solid contour lines correspond to the exact spreading surface, while the dashed contour lines correspond to the approximate spreading surface.