|
|
|
|
Wave-equation migration velocity analysis for VTI media using optimized implicit finite difference |
Yunyue (Elita) Li
 and
and 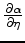 are mapped into two finite difference coefficients,
are mapped into two finite difference coefficients, 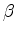 and
and 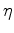 .
When computing the perturbed wavefields from model perturbation, I apply a chain rule to link the
wave equation with the actual anisotropic parameters via the finite difference coefficients. I test
the implementation by impulse responses in both 2D and 3D. The sensitivity kernels for wave-equation
reflection tomography confirm the theoretical understanding that waves have a higher sensitivity
for
.
When computing the perturbed wavefields from model perturbation, I apply a chain rule to link the
wave equation with the actual anisotropic parameters via the finite difference coefficients. I test
the implementation by impulse responses in both 2D and 3D. The sensitivity kernels for wave-equation
reflection tomography confirm the theoretical understanding that waves have a higher sensitivity
for  at large angles and a higher sensitivity for vertical velocity at small angles.
at large angles and a higher sensitivity for vertical velocity at small angles.
|
|
|
|
Wave-equation migration velocity analysis for VTI media using optimized implicit finite difference |