|
|
|
|
Wave-equation migration velocity analysis for VTI media using optimized implicit finite difference |
Therefore, I use an optimized implicit finite difference propagator first developed by
Shan (2006). In this optimized implicit finite difference scheme, the anisotropic
parameters  and
and 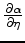 contribute to the wave-equation implicitly via two finite difference
parameters
contribute to the wave-equation implicitly via two finite difference
parameters 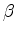 and
and 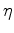 . Tables of
. Tables of 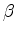 and
and 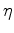 with respect to sets of discrete
with respect to sets of discrete
 and
and 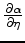 values are precomputed before propagation by minimizing the difference between
the true dispersion relationship and its rational series approximation at different wavenumbers.
This table-driven, implicit finite difference method handles lateral variations and is accurate
up to
values are precomputed before propagation by minimizing the difference between
the true dispersion relationship and its rational series approximation at different wavenumbers.
This table-driven, implicit finite difference method handles lateral variations and is accurate
up to 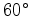 in a vertical transverse isotropic (VTI) medium.
in a vertical transverse isotropic (VTI) medium.
When perturbing the wave-equation around its current state, the finite difference coefficients 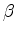 and
and 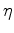 are perturbed. These perturbations are then translated into the anisotropic parameters
are perturbed. These perturbations are then translated into the anisotropic parameters  and
and 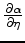 using the chain rule. Tables of numerical derivatives of the finite difference coefficients
using the chain rule. Tables of numerical derivatives of the finite difference coefficients 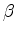 and
and 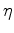 with respect to the anisotropic parameter
with respect to the anisotropic parameter  are also precomputed from the previous coefficients
tables.
are also precomputed from the previous coefficients
tables.
Finally, I test this implicit finite difference implementation by 2D and 3D impulse responses for
vertical velocity 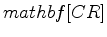 and
and  . The results verify the theoretical understanding of the WEMVA operator
for anisotropic models.
. The results verify the theoretical understanding of the WEMVA operator
for anisotropic models.
|
|
|
|
Wave-equation migration velocity analysis for VTI media using optimized implicit finite difference |