




Next: Conclusions
Up: INTRODUCING THE OFFSET CONTINUATION
Previous: Offset continuation geometry: time
This section discusses the connection between the laws of traveltime
transformation and the laws of the corresponding amplitude transformation.
The change of the wave amplitudes in the OC process is described by
the first-order partial differential transport equation (6). The
general solution of this equation can be found by applying
the method of
characteristics. It takes the
explicit integral form
| 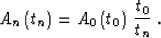 |
(30) |
The integral in (30) is defined on a curved time ray, and An(tn)
stands for the amplitude transported along this ray. In the case of a plane
dipping reflector, the ray amplitude can be immediately evaluated by
substituting the explicit traveltime and time ray formulas from the
preceding section into (30). The amplitude expression in
this case takes the simple form
| 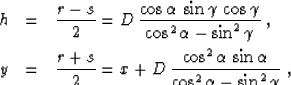 |
(31) |
In order to consider the more general case of a curvilinear reflector,
we need to
take into account a connection between the traveltime
derivatives in (30) and the geometric quantities of the reflector.
As follows directly from the trigonometry of the incident and reflected rays
triangle (Figure 1),
| 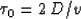 |
(32) |
| (33) |
| (34) |
where D is the length of the normal ray. Let 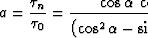 be the
zero-offset reflection traveltime. Combining (32) and (34) with
(10) we can get the following relationship:
be the
zero-offset reflection traveltime. Combining (32) and (34) with
(10) we can get the following relationship:
| 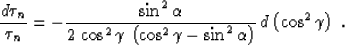 |
(35) |
which interprets the ``DMO smile'' (28) found by Deregowski
and Rocca
1981 in geometric terms. Equation (35)
allows a convenient change of variables in (30). Let the
reflection angle 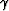 be a parameter monotonously increasing along a time
ray. In this case, each time ray is uniquely determined by the position of the
reflection point, which in turn is defined by the values of D and
be a parameter monotonously increasing along a time
ray. In this case, each time ray is uniquely determined by the position of the
reflection point, which in turn is defined by the values of D and
 . According to this change of variables we can differentiate (35)
along a time ray to get
. According to this change of variables we can differentiate (35)
along a time ray to get
| 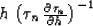 |
(36) |
Note also that the quantity 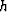 in (30) coincides exactly with the time ray invariant
C3 found in (18). Therefore its value is constant along each time ray
and equals
in (30) coincides exactly with the time ray invariant
C3 found in (18). Therefore its value is constant along each time ray
and equals
| 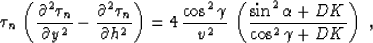 |
(37) |
Finally, as shown in Appendix B,
| 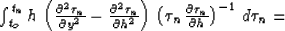 |
(38) |
where K is the reflector curvature at the reflection point. Substituting
(36), (37), and (38) into (30) transforms
the integral
to the form
| 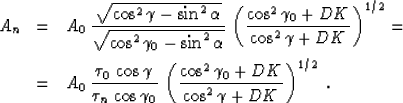 |
(39) |
which we can evaluate analytically. The final formula for the
amplitude transformation takes the form
| 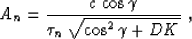 |
|
| (40) |
In case of a plane reflector, the curvature K is zero, and (40)
coincides with (31). Equation (40) can be rewritten as
| 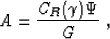 |
(41) |
where c is constant along each time ray (it may vary with the reflection point
location on the reflector but not with the offset). We should compare equation
(41)
with the known expression for the reflection wave amplitude of the leading
ray series term in 2.5-D media:
| 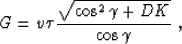 |
(42) |
where CR stands for the angle-dependent reflection coefficient, G is the
geometric spreading
| 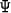 |
(43) |
and 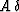 includes other possible factors (such as the source directivity)
that we can either correct or neglect in the preliminary processing.
It is evident that the curvature dependence of the amplitude transformation
(41) coincides completely with the true geometric spreading factor
(43), and that the angle dependence of the reflection coefficient is not
provided by the offset continuation process. If the wavelet shape of the
reflected wave on seismic sections (Rn in (4)) is described
by the delta function, then, as follows from the known properties of
this function,
includes other possible factors (such as the source directivity)
that we can either correct or neglect in the preliminary processing.
It is evident that the curvature dependence of the amplitude transformation
(41) coincides completely with the true geometric spreading factor
(43), and that the angle dependence of the reflection coefficient is not
provided by the offset continuation process. If the wavelet shape of the
reflected wave on seismic sections (Rn in (4)) is described
by the delta function, then, as follows from the known properties of
this function,
| 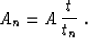 |
(44) |
which leads to the equality
| 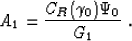 |
(45) |
Combining (45) with (42) and (41) allows us to
evaluate the amplitude after continuation from some initial offset h0 to
another offset h1, as follows:
| 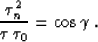 |
(46) |
Equation (46) indicates that the OC process described by equation
(1) is amplitude-preserving in the sense that corresponds to the
so-called Born DMO Bleistein (1990); Liner (1991). This means that
the geometric spreading factor from the initial amplitudes is transformed to
the
true geometric spreading on the continued section, while the reflection
coefficient stays the same. This remarkable dynamic property allows AVO
(amplitude versus offset) analysis to be performed by a dynamic comparison
between true constant-offset sections and the sections transformed by OC from
different offsets. With a simple trick, the offset coordinate is
transferred to the reflection
angles for the AVO analysis.
As follows from (35) and (10),
| 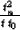 |
(47) |
If we include the 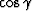 factor in the DMO operator
(continuation to zero offset) and divide the result by the DMO
section obtained without this factor, the resultant amplitude of the reflected
events
will be directly proportional to
factor in the DMO operator
(continuation to zero offset) and divide the result by the DMO
section obtained without this factor, the resultant amplitude of the reflected
events
will be directly proportional to 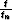 , where the reflection angle
, where the reflection angle
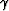 corresponds to the initial offset. Of course, this conclusion is
rigorously
valid for constant-velocity 2.5-D media only.
corresponds to the initial offset. Of course, this conclusion is
rigorously
valid for constant-velocity 2.5-D media only.
Black et al. 1993 recently suggested a definition of
true-amplitude DMO different from that of Born DMO. The difference
consists of
two important components:
- 1.
- True-amplitude DMO addresses preserving the peak amplitude of the
image wavelet instead of preserving its spectral density.
In the terms of this
paper, the peak amplitude corresponds to the initial amplitude A instead of
the spectral density amplitude An. A simple correction factor
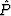 would help us
take the difference between the two amplitudes into account. Multiplication by
would help us
take the difference between the two amplitudes into account. Multiplication by
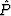 can be easily done at the NMO stage.
can be easily done at the NMO stage.
- 2.
- Seismic sections are multiplied by time to correct for the geometric
spreading factor prior to DMO (or in our case, offset continuation)
processing.
As follows from (43), multiplication by t is a valid geometric
spreading correction for plane reflectors only.
It is amplitude-preserving
offset continuation based on the OC equation (1) that
is able to correct
for the curvature-dependent factor in the amplitude. To take into account
the second aspect of Black's definition, we can consider the wave
field  such
that
such
that
| 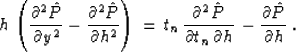 |
(48) |
Substituting (48) into the OC equation (1) transforms the
latter to the form
| 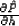 |
(49) |
Equations (49) and (1) differ only with
respect to the first-order term  .This term affects
the amplitude behavior but not the traveltimes, since the
eikonal-type equation (5) depends on the second-order terms only.
Offset continuation operators based on (49) conform to
Black's definition of true-amplitude processing.
.This term affects
the amplitude behavior but not the traveltimes, since the
eikonal-type equation (5) depends on the second-order terms only.
Offset continuation operators based on (49) conform to
Black's definition of true-amplitude processing.





Next: Conclusions
Up: INTRODUCING THE OFFSET CONTINUATION
Previous: Offset continuation geometry: time
Stanford Exploration Project
6/19/2000
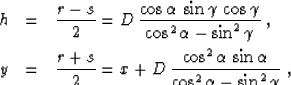
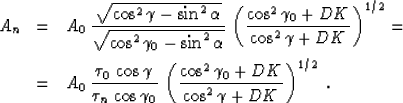
 such
that
such
that
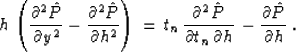
 .This term affects
the amplitude behavior but not the traveltimes, since the
eikonal-type equation (5) depends on the second-order terms only.
Offset continuation operators based on (49) conform to
Black's definition of true-amplitude processing.
.This term affects
the amplitude behavior but not the traveltimes, since the
eikonal-type equation (5) depends on the second-order terms only.
Offset continuation operators based on (49) conform to
Black's definition of true-amplitude processing.