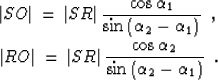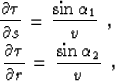Next: Offset continuation geometry: time
Up: INTRODUCING THE OFFSET CONTINUATION
Previous: INTRODUCING THE OFFSET CONTINUATION
In order to prove the validity of equation (5), it is
convenient to transform it
to the coordinates of the initial shot gathers: s=y-h, r=y+h, and
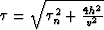 . The transformed equation takes the
form
. The transformed equation takes the
form
| 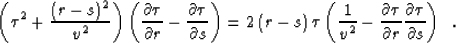 |
(7) |
Now the goal is to prove that any reflection traveltime function
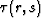 in a constant velocity medium satisfies equation (7).
in a constant velocity medium satisfies equation (7).
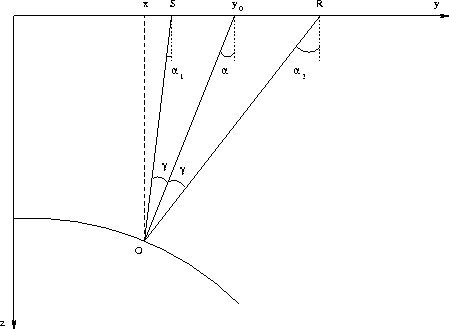
Let S and R be the source and the reflection locations, and O be
a reflection point for that pair.
Note that the incident ray SO and the reflected ray
OR form a triangle with the basis on the offset SR (l=|SR|=r-s).
Let
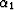 be the angle of SO from the vertical axis, and
be the angle of SO from the vertical axis, and 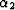 be the
analogous angle of RO (Figure 1). Elementary trigonometry
(the law of sines)
gives us the following explicit relationships between the sides and
the angles of
the triangle SOR:
be the
analogous angle of RO (Figure 1). Elementary trigonometry
(the law of sines)
gives us the following explicit relationships between the sides and
the angles of
the triangle SOR:
| 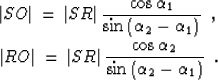 |
(8) |
| (9) |
Hence, the total length of the reflected ray is
| 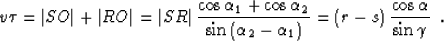 |
(10) |
Here 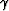 is the reflection angle (
is the reflection angle (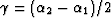 ), and
), and  is the central ray angle (
is the central ray angle (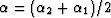 ) coincident with the local dip angle of the reflector at
the reflection point.
Recalling the well-known relationships between the ray angles and the
first-order traveltime derivatives
) coincident with the local dip angle of the reflector at
the reflection point.
Recalling the well-known relationships between the ray angles and the
first-order traveltime derivatives
| 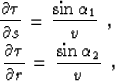 |
(11) |
| (12) |
we can substitute (10), (11), and (12) into
(7), which leads to the simple trigonometric equality
| 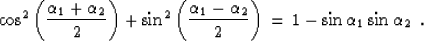 |
(13) |
It is now easy to prove that equality (13) is true for any
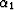 and
and 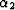 .
.
ocoray
Figure 1 Reflection rays in a constant
velocity medium (a scheme).
|
|  |

Thus we have proved that equation
(7), equivalent to (5), is valid in constant
velocity media independently of the reflector geometry and the offset.
This means that high-frequency asymptotic components of the waves,
described by the OC equation,
are located on the true reflection traveltime curves.
The theory of characteristics can provide other ways to prove the kinematic
validity of equation (5), as described in Fomel (1994); Goldin (1994).





Next: Offset continuation geometry: time
Up: INTRODUCING THE OFFSET CONTINUATION
Previous: INTRODUCING THE OFFSET CONTINUATION
Stanford Exploration Project
6/19/2000
![]() . The transformed equation takes the
form
. The transformed equation takes the
form
![]() be the angle of SO from the vertical axis, and
be the angle of SO from the vertical axis, and ![]() be the
analogous angle of RO (Figure 1). Elementary trigonometry
(the law of sines)
gives us the following explicit relationships between the sides and
the angles of
the triangle SOR:
be the
analogous angle of RO (Figure 1). Elementary trigonometry
(the law of sines)
gives us the following explicit relationships between the sides and
the angles of
the triangle SOR: