




Next: Discussion
Up: Continuous case and seismic
Previous: Continuous case and seismic
It is interesting to note that a wide class of integral operators,
routinely used in seismic data processing, have the form of operator
(22) with the ``Green'' function
| 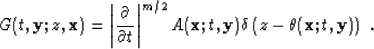 |
(24) |
where we have split the variable x into the one-dimensional
component z (typically depth or time) and the m-dimensional
component  (typically a lateral coordinate with m equal
1 or 2.) Similarly, the variable y is split into t and
(typically a lateral coordinate with m equal
1 or 2.) Similarly, the variable y is split into t and
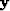 . The function
. The function 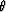 represents the summation
path , which captures the kinematic properties of the operator, and
A is the amplitude function.
represents the summation
path , which captures the kinematic properties of the operator, and
A is the amplitude function.
Impulse response (27) is typical for different forms of
Kirchhoff migration and datuming as well as for velocity transform,
integral offset continuation, DMO, and AMO. Integral operators of that
class rarely satisfy the unitarity condition, with Radon transform
(slant stack) being a notable exception. In an earlier paper
Fomel (1996), I have shown that it is possible to define
the amplitude function A for each kinematic path 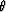 so that
the operator becomes asymptotic pseudo-unitary . This means that
the adjoint operator coincides with the inverse in the high-frequency
(stationary-phase) approximation. Consequently, equation
(25) is satisfied to the same asymptotic order.
so that
the operator becomes asymptotic pseudo-unitary . This means that
the adjoint operator coincides with the inverse in the high-frequency
(stationary-phase) approximation. Consequently, equation
(25) is satisfied to the same asymptotic order.
Using asymptotic pseudo-unitary operators, we can apply formula
(26) to find an explicit analytic form of the interpolation
function W, as follows:
| 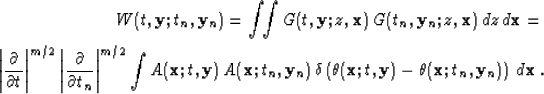 |
|
| (25) |
Here the amplitude function A is defined according to the general
theory of asymptotic pseudo-inverse operators as
| 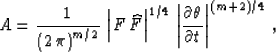 |
(26) |
where
| 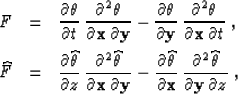 |
(27) |
| (28) |
and 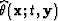 is the dual
summation path, obtained by solving equation
is the dual
summation path, obtained by solving equation 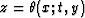 for t
(assuming that an explicit solution is possible).
for t
(assuming that an explicit solution is possible).
For a simple example, let us consider the case of zero-offset time
migration with a constant velocity v. The summation path 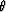 in this case is an ellipse
in this case is an ellipse
| 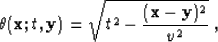 |
(29) |
and the dual summation path 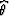 is a hyperbola
is a hyperbola
| 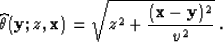 |
(30) |
The corresponding pseudo-unitary amplitude function is found from
formula (29) to be Fomel (1996)
| 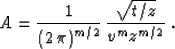 |
(31) |
Substituting formula (34) into (28), we derive
the corresponding interpolation function
| 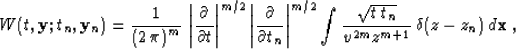 |
(32) |
where 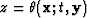 , and
, and 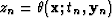 . For m=1 (the two-dimensional
case), we can apply the known properties of the delta function to
simplify formula (35) further to the form
. For m=1 (the two-dimensional
case), we can apply the known properties of the delta function to
simplify formula (35) further to the form
| ![\begin{displaymath}
W
= \frac{v}{\pi} \,
\left\vert\frac{\partial}{\partial t...
...
\left[v^2 (t + t_n)^2 - (\bold{y}-\bold{y}_n)^2\right]
}}\;.\end{displaymath}](img57.gif) |
(33) |
The result is an interpolator for zero-offset seismic sections. Like
the sinc interpolator in formula (19) that is based on
decomposing the signal into sinusoids, interpolation (36)
is based on decomposing the zero-offset section into hyperbolas.





Next: Discussion
Up: Continuous case and seismic
Previous: Continuous case and seismic
Stanford Exploration Project
9/12/2000
![]() so that
the operator becomes asymptotic pseudo-unitary . This means that
the adjoint operator coincides with the inverse in the high-frequency
(stationary-phase) approximation. Consequently, equation
(25) is satisfied to the same asymptotic order.
so that
the operator becomes asymptotic pseudo-unitary . This means that
the adjoint operator coincides with the inverse in the high-frequency
(stationary-phase) approximation. Consequently, equation
(25) is satisfied to the same asymptotic order.
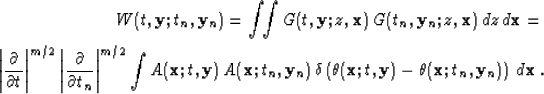
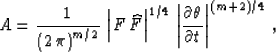
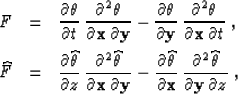
![]() in this case is an ellipse
in this case is an ellipse
![\begin{displaymath}
W
= \frac{v}{\pi} \,
\left\vert\frac{\partial}{\partial t...
...
\left[v^2 (t + t_n)^2 - (\bold{y}-\bold{y}_n)^2\right]
}}\;.\end{displaymath}](img57.gif)