




Next: Acknowledgments
Up: Fomel: Interpolation
Previous: Asymptotic pseudo-unitary operators as
A simple linear interpolation theory can be derived from the sole
principle of function bases. The choice of a function basis for the
interpolated data uniquely defines a linear interpolation operator.
In application to seismic data interpolation, the basis set of
functions can be given by the Green functions of an imaging
operator, such as prestack migration or DMO. The linear
interpolation operator in this case is intimately related to the
general formulation of azimuth moveout (AMO). Some of the
conclusions that the general theory can supply for AMO are
- In interpolation problems, the accuracy of operators (e.g.
taking into account anisotropy, velocity variations, etc.) is of
minor importance as long as the operator provides a complete basis
set for describing the data.
- Formula (26) stresses the importance of using unitary
operators (orthonormal bases) to construct linear interpolation. It
suggests that unitary operators are even more important in
interpolation problems than ``true-amplitude'' operators. Though
applying non-orthogonal bases in interpolation problems is
theoretically possible, it requires an intrinsic inversion of the
matrix operator
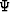 , defined in formulas (9) or
(24). Such an inversion is rarely feasible in practice.
The theory of asymptotic pseudo-unitary operators
Fomel (1996) supplies a useful tool for constructing
asymptotically orthonormal bases.
, defined in formulas (9) or
(24). Such an inversion is rarely feasible in practice.
The theory of asymptotic pseudo-unitary operators
Fomel (1996) supplies a useful tool for constructing
asymptotically orthonormal bases.
- It is also important to seek the most compact set of basis
functions, e.g., the fewest number of frequencies in the spectrum.
The Green functions may correspond to the solutions of a partial
differential equation. The frequencies, actually present in the
data, may correspond to the zeroes of the prediction-error filter.
More challenging research needs to be done in relating differential
equations, prediction filters, and function bases.
How is the mathematical theory of interpolation related to the
problem of interpolating irregularly sampled data? The theory
provides a linear interpolation operator 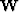 , defined in
formula (1) and evaluated in formula
(13). What we actually need to consider is a linear
equation
, defined in
formula (1) and evaluated in formula
(13). What we actually need to consider is a linear
equation
| 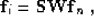 |
(34) |
where 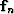 represents the desired regularly sampled output,
represents the desired regularly sampled output,
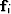 denotes the recorded irregularly spaced data, and
denotes the recorded irregularly spaced data, and
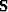 is the sampling operator. Estimating
is the sampling operator. Estimating 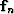 from (37) requires the art and science of linear
inversion, which includes such tools as regularization and
preconditioning.
from (37) requires the art and science of linear
inversion, which includes such tools as regularization and
preconditioning.





Next: Acknowledgments
Up: Fomel: Interpolation
Previous: Asymptotic pseudo-unitary operators as
Stanford Exploration Project
9/12/2000
![]() , defined in
formula (1) and evaluated in formula
(13). What we actually need to consider is a linear
equation
, defined in
formula (1) and evaluated in formula
(13). What we actually need to consider is a linear
equation