




Next: Discrete Fourier basis
Up: Interpolation with Fourier basis
Previous: Interpolation with Fourier basis
For the continuous Fourier transform, the set of basis functions is
defined by
| 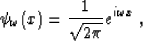 |
(15) |
where 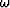 is the continuous frequency. For a 1-point
sampling interval, the frequency is limited by the Nyquist
condition:
is the continuous frequency. For a 1-point
sampling interval, the frequency is limited by the Nyquist
condition: 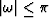 . In this case, the interpolation
function W can be computed from formula (13) to be
. In this case, the interpolation
function W can be computed from formula (13) to be
| ![\begin{displaymath}
W (x, n) = \frac{1}{2 \pi} \int_{-\pi}^{\pi} e^{i \omega (x...
...\omega = \frac{\sin \left[\pi (x - n) \right]}{\pi (x - n)} \;.\end{displaymath}](img27.gif) |
(16) |
The interpolation function (19) is well-known as the
Shannon sinc interpolator. A known problem with its practical
implementation is the slow decay with (x - n). This problem is
solved in practice with heuristic tapering Hale (1980),
such as Harlan's triangle tapering Harlan (1982). While
the function W from equation (19) automatically
satisfies properties (3) and (17), where
both x and n range from 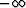 to
to 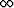 , its tapered
version may require additional normalization.
, its tapered
version may require additional normalization.





Next: Discrete Fourier basis
Up: Interpolation with Fourier basis
Previous: Interpolation with Fourier basis
Stanford Exploration Project
9/12/2000