To perform reflection tomography,
in addition to ray tracing,
we need to compute the gradient of
traveltimes with respect to the velocity function
and to handle correctly the reflections at the boundaries.
Appendix A shows the relationships between
the ray parameters
of the incident and reflected ![]() -rays at a planar interface.
In this section we derive the traveltime gradients
for
-rays at a planar interface.
In this section we derive the traveltime gradients
for ![]() -rays.
The derivation is straightforward and is based
on Fermat principle applied to the
-rays.
The derivation is straightforward and is based
on Fermat principle applied to the ![]() -rays.
-rays.
The transformation of variables
defined in equations (2) and (3)
implies the following relationships between
the differential quantities ![]() and
and ![]() .
.
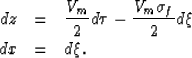 |
(13) | |
| (14) |
Applying this transformations to the expression
of the time increment along a z-ray,
leads to the equivalent expression for the
the time increment along a ![]() -ray,
-ray,
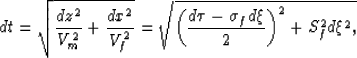 |
(15) |
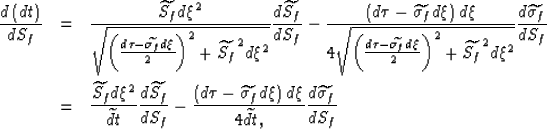 |
(16) | |
| (17) |
Applying Fermat principle,
the first order perturbations in the traveltimes
![]() caused by
perturbations in slowness
caused by
perturbations in slowness ![]() are given by the following
integral evaluated along the unperturbed raypath
are given by the following
integral evaluated along the unperturbed raypath ![]() -ray,
-ray,
| (18) |