




Next: Comparing linearizations of forward
Up: Reflection tomography in
Previous: Reflection tomography in
One of the most challenging problems of reflection tomography
is to track correctly the movement of reflectors
caused by changes in velocity.
Usually the reflectors are parametrized
independently from velocity and
large reflectors movement can cause
instability in the inversion process.
One of the potential advantages of 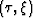 tomography over
tomography over 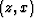 tomography is that
reflectors move less in the
tomography is that
reflectors move less in the 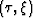 than in the
than in the
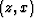 domain,
and that they move more consistently with the velocity
function.
domain,
and that they move more consistently with the velocity
function.
This reflector movement caused by velocity
perturbations can be subdivided
in a residual migration component and a
residual mapping component.
One of the advantages of 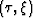 tomography is that
the residual mapping is automatically taken
into account by the linearization
introduced in equation (17).
In contrast,
tomography is that
the residual mapping is automatically taken
into account by the linearization
introduced in equation (17).
In contrast,
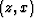 tomography
has an additional term to take into
account both the residual mapping and migration effects.
In the examples
shown in this paper we used the following
adaptation of the expression presented by
Stork and Clayton 1991
to correct for the residual mapping in
tomography
has an additional term to take into
account both the residual mapping and migration effects.
In the examples
shown in this paper we used the following
adaptation of the expression presented by
Stork and Clayton 1991
to correct for the residual mapping in 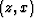 tomography:
tomography:
| 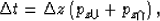 |
(19) |
where
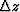 is the reflector vertical movement,
while
is the reflector vertical movement,
while
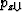 and
and 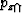 are respectively the vertical
ray parameters of the incident and reflected rays
at the reflection point.
To be consistent in the comparison between
are respectively the vertical
ray parameters of the incident and reflected rays
at the reflection point.
To be consistent in the comparison between 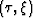 domain tomography and
domain tomography and 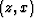 domain tomography,
we computed
domain tomography,
we computed 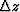 as a residual mapping term
along the vertical path.
The residual migration term could be computed by performing
a residual map migration of the zero-offset arrivals.
This residual migration term could be added to both
as a residual mapping term
along the vertical path.
The residual migration term could be computed by performing
a residual map migration of the zero-offset arrivals.
This residual migration term could be added to both
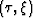 domain tomography and
domain tomography and 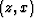 domain tomography.
For
domain tomography.
For 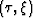 tomography
the expression linking the
tomography
the expression linking the 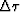 caused by residual migration to the
corresponding traveltime perturbations
would be similar to equation (19);
that is,
caused by residual migration to the
corresponding traveltime perturbations
would be similar to equation (19);
that is,
| 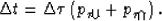 |
(20) |





Next: Comparing linearizations of forward
Up: Reflection tomography in
Previous: Reflection tomography in
Stanford Exploration Project
5/1/2000
![]() tomography is that
the residual mapping is automatically taken
into account by the linearization
introduced in equation (17).
In contrast,
tomography is that
the residual mapping is automatically taken
into account by the linearization
introduced in equation (17).
In contrast,
![]() tomography
has an additional term to take into
account both the residual mapping and migration effects.
In the examples
shown in this paper we used the following
adaptation of the expression presented by
Stork and Clayton 1991
to correct for the residual mapping in
tomography
has an additional term to take into
account both the residual mapping and migration effects.
In the examples
shown in this paper we used the following
adaptation of the expression presented by
Stork and Clayton 1991
to correct for the residual mapping in ![]() tomography:
tomography: