Focusing eikonal equation

To derive the focusing eikonal equation we apply a coordinates transformation from depth (z) to two-ways vertical traveltime $(\tau)$to the eikonal of the acoustic wave equation. The eikonal for the arrival time t of high-frequency acoustic waves is

 

$$V_m\left(z,x\right)^2 \left[ \frac{\partial t\left(z,x\righ... ... \frac{\partial t\left(z,x\right)} {\partial x} \right]^2 = 1,$$ (1)

where V_m and V_f are respectively the mapping velocity and the focusing velocity. Because we are interested to analyze the effects of focusing and mapping velocities on reflection traveltimes, we kept the V_f and V_m distinguished in equation (1). Although this equation is valid for a general elliptical anisotropic medium, in this paper we focus on isotropic media. A companion paper discusses the focusing eikonal for a general transversely isotropic media with a vertical axis of symmetry. Alkhalifah et al. (1997).

The mapping between the depth $\left(z,x\right)$ and the vertical traveltime $\left(\tau,\xi\right)$ domain are defined by the following transformation of coordinates:

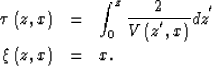$$\begin{eqnarray} \tau \left( z,x\right) &=& \int_{0}^{z} \frac{2}{V\left(z^{'},x\right)} dz^{'} \\ \xi \left( z,x\right) &=& x.\end{eqnarray}$$ (2) (3)

This transformation implies the following relationships between the partial derivatives of the traveltime that appear in the eikonal equation (1):

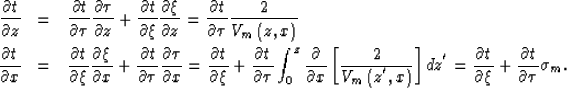$$\begin{eqnarray} \frac{\partial t}{\partial z} & = & \frac{\partial t}{\partia... ...al t }{\partial \xi } + \frac{\partial t}{\partial \tau} \sigma_m.\end{eqnarray}$$ (4) (5)

Substituting these partial derivatives in the eikonal equation (1) we derive the focusing eikonal equation

$$4 \left[ \frac{\partial t\left(\tau,\xi\right)} {\partial \... ...{\partial t\left(\tau,\xi\right)} {\partial \tau} \right]^2=1.$$ (6)

The focusing eikonal depends directly from the the focusing velocity but only indirectly from the mapping velocity, through the differential mapping factor $\sigma_m$. Furthermore, because $\sigma_m$ is the vertical integral of the horizontal derivative of V_m, when V_m is assumed to be proportional to V_f with a constant of proportionality that is only function of depth; that is,  

$$V_m\left(z,x\right)=\alpha\left(z\right) V_f\left(z,x\right),$$ (7)

the focusing eikonal becomes independent from V_m.

This property is easily demonstrated by performing the change of variable from z to $\tau$ defined in equation (2) in the integral that defines $\sigma_m$in equation (5). After this change of variable the expression for $\sigma_m$ as a function of $\tau$ becomes

$$\begin{eqnarray} \sigma_m\left(\tau,x\right) &=& \int_{0}^{\tau} V_m\left(\tau^... ...l x} \left[\frac{1}{V_f\left(\tau^{'},x\right)}\right] d\tau^{'}.\end{eqnarray}$$ (8)

In the companion paper 1997 we analyze the errors caused by assuming $\sigma_m$ equal to $\sigma_f$when the condition of equation (7) in not exactly fulfilled.

The previous result demonstrates that, as long as the condition of equation (7) is satisfied, reflection data can be focused without knowledge of the mapping velocity, and thus that the focusing step and the mapping step can be performed sequentially.

Notice that in an horizontally stratified medium the focusing eikonal becomes the eikonal for an elliptical anisotropic medium with normalized vertical ``velocity'' equal to 2. If the velocity is laterally varying, neglecting $\sigma_f$ is equivalent to neglecting the thin-lens term in finite-difference time migration Hatton et al. (1981). Raynaud and Thore 1993 used this approximation to trace rays in the $\tau$ domain.

The presence of the differential mapping factor $\sigma_f$in the focusing eikonal makes the separation of the mapping and the focusing processes imperfect. Therefore the eikonal in equation (1) should be properly called quasi-focusing. An interesting development would be to substitute for the transformation of variables defined by equations (2) and (3) a different transformation of variables for which $\sigma_f$ would be uniformly zero even in a laterally varying medium. We speculate that this transformation of variable is the one induced by the image rays Hubral (1977).

Finally we should notice that the expressions for evaluating $\sigma_f$ given in equation (5), or even in equation (8), are not convenient when working in the $\left(\tau,\xi\right)$ domain, because they require the evaluation of spatial derivatives in the $\left(z,x\right)$.It can be easily demonstrated that $\sigma_f$ can be evaluated using the following expression,

 

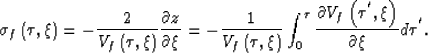$$\sigma_f\left(\tau,\xi\right) = -\frac{2}{V_f\left(\tau,\xi\... ...rtial {V_f\left(\tau^{'},\xi\right)}} {\partial \xi} d\tau^{'}.$$ (9)