Orthogonality of the gradients

The orthogonality principle (25) transforms according to the dot-product test (27) to the form  

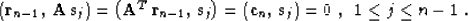$$\left({\bf r}_{n-1},\,{\bf A\,s}_{j}\right) = \left({\bf A}... ...{\bf c}_{n},\,{\bf s}_{j}\right) = 0\;,\;\;1 \leq j \leq n-1\;.$$ (29)

Forming the dot product 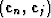$\left({\bf c}_{n},\,{\bf c}_{j}\right)$ and applying formula (22), we can see that  

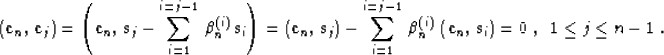$$\left({\bf c}_{n},\,{\bf c}_{j}\right) = \left({\bf c}_{n},\... ...{\bf c}_{n},\,{\bf s}_{i}\right) = 0\;,\;\;1 \leq j \leq n-1\;.$$ (30)

Equation (30) proves the orthogonality of the gradient directions from different iterations. Since the gradients are orthogonal, after n iterations they form a basis in the n-dimensional space. In other words, if the model space has n dimensions, each vector in this space can be represented by a linear combination of the gradient vectors formed by n iterations of the conjugate-gradient method. This is true as well for the vector 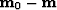${\bf m}_0 - {\bf m}$, which points from the solution of equation (1) to the initial model estimate ${\bf m}_0$. 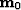Neglecting computational errors, it takes exactly n iterations to find this vector by successive optimization of the coefficients. This proves that the conjugate-gradient method converges to the exact solution in a finite number of steps (assuming that the model belongs to a finite-dimensional space).

The method of conjugate gradients simplifies formula (26) to the form  

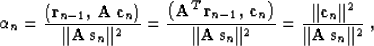$$\alpha_n = {{\left({\bf r}_{n-1},\,{\bf A\,c}_n\right)} \ove... ...= {{\Vert{\bf c}_n\Vert^2} \over {\Vert{\bf A\,s}_n\Vert^2}}\;,$$ (31)

which in turn leads to the simplification of formula (8), as follows:  

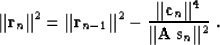$$\Vert{\bf r}_n\Vert^2 = \Vert{\bf r}_{n-1}\Vert^2 - {{\Vert{\bf c}_n\Vert^4}\over {\Vert{\bf A\,s}_n\Vert^2}}\;.$$ (32)

If the gradient is not equal to zero, the residual is guaranteed to decrease. If the gradient is equal to zero, we have already found the solution.