Next: PROGRAM
Up: WHAT ARE ADJOINTS FOR?
Previous: Orthogonality of the gradients
Substituting the gradient direction (28) into formula
(23) and applying formulas (4) and (27), we can
see that
| 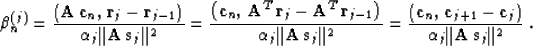 |
(33) |
The orthogonality condition (30) and the definition of the
coefficient 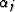 from equation (31) further transform this formula
to the form
from equation (31) further transform this formula
to the form
| 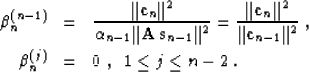 |
(34) |
| (35) |
Equation (35) shows that the conjugate-gradient method needs
to remember only the previous step direction in order to optimize the
search at each iteration. This is another remarkable property
distinguishing that method in the family of conjugate-direction
methods.





Next: PROGRAM
Up: WHAT ARE ADJOINTS FOR?
Previous: Orthogonality of the gradients
Stanford Exploration Project
9/11/2000