Discussion

At this point, we would like to express a word of caution and remind the reader of some well known facts Claerbout (1976):

1.

Not all functions are possible auto or cross-spectra.

2.

Every given auto or cross-correlation function has an infinite number of possible solutions, of which there is a unique minimum phase wavelet (or pair of wavelets for cross-correlations) except for a complex scale factor of unit magnitude.

3.

Let S(Z) be the Z transform representation of an auto-correlation function. Suppose that we have a way to determine the roots of such a polynomial of order 2N: Z^N S(Z)=0. We can now check to see if the roots come in pairs Z and 1/Z, i.e. if there is a root outside of the unit circle for every root inside. If this is true, we have a spectrum, and the roots outside of the unit circle are the actual roots of the minimum phase factor (Figure 1). If we don't have roots mirroring each other with respect to the unit circle, then we don't really have a spectrum, and we shouldn't even try to factorize it (Figure 2).

 

lapl4 Figure 1 Roots of the Z transform representation of a Laplacian: P(Z)=ZN(-Z-N-Z-1+4-Z1-ZN). No roots are on the unit circle, except for Z=1 and all the roots appear in pairs that mirror each other with respect to the unit circle.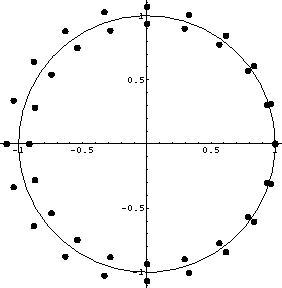

 

lapl3 Figure 2 Roots of the Z transform representation of a pseudo-Laplacian:P(Z)=ZN(-Z-N-Z-1+3-Z1-ZN) Some of the roots are on the unit circle, therefore this is not a spectrum, and so it is not factorizable.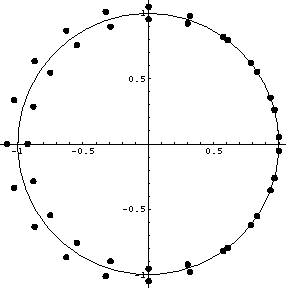

A special case occurs when we have a pair of roots on the unit circle (see, for example, Z=1, Figure 1). A polynomial of this type can be factorized into minimum phase causal and anticausal parts, but the convergence of the Wilson-Burg algorithm becomes linear instead of quadratic and it may even get unstable, as originally pointed out by Wilson 1969.