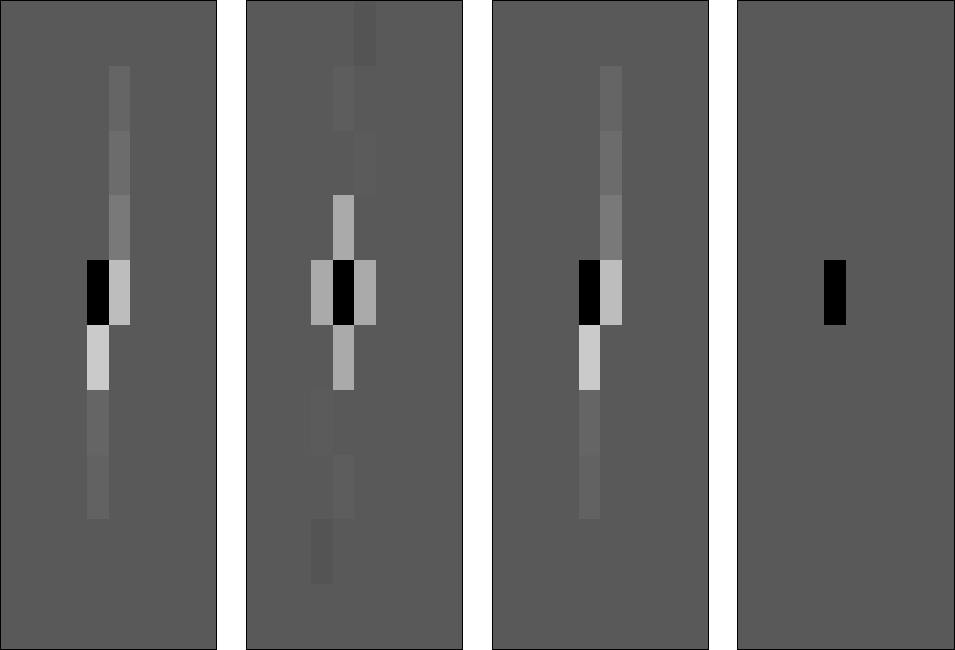Example

In a first example, we applied the method to deconvolution on the helix Claerbout (1997) using the factors obtained with the Wilson-Burg spectral factorization. We take the auto-correlation to be the negative of the Laplacian operator, and convolve it with a spike placed in the middle of each panel in Figure 3. We use the Wilson-Burg method to find the wavelet with this auto-correlation and then deconvolve (do polynomial division) on the helix to find back the input spike.

 

autolapfac
Figure 3 Wilson factorization of the Laplacian. From left to right: the input filter; its auto-correlation; the factors obtained with the Wilson-Burg method; the result of the deconvolution using the Wilson-Burg factors.

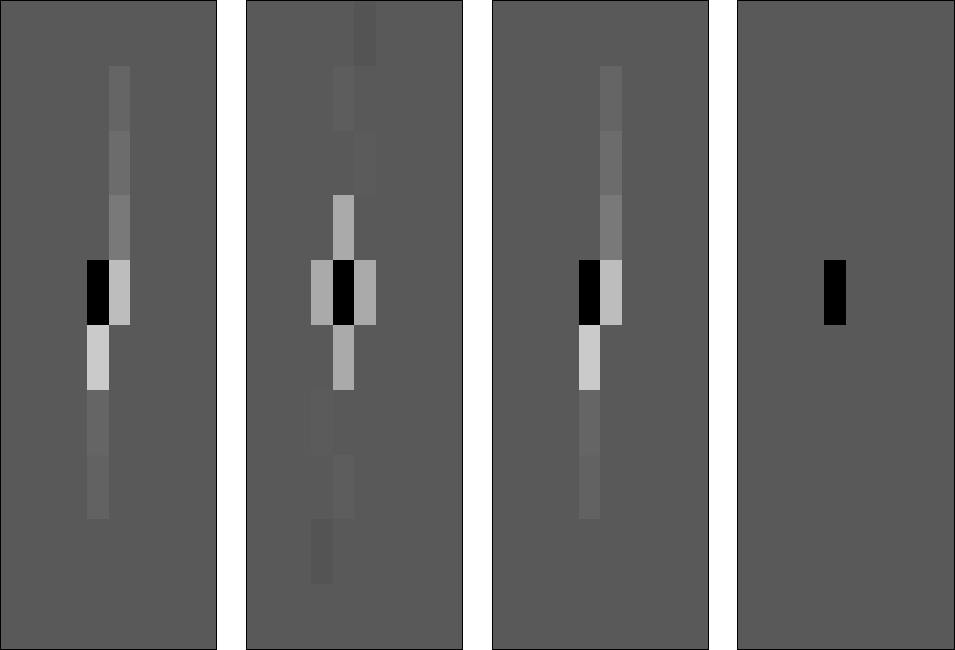In another example, we analyzed the rate of convergence of the Wilson-Burg method. We selected a simple polynomial which is the cross-correlation of two triangle functions,

$$4/Z+15+11Z+7Z^2+3Z^3 = 12\; \left(1+\frac{1}{3Z}\right) \left(1+\frac{3}{4}Z+\frac{1}{2}Z^2+\frac{1}{4}Z^3\right)$$ (14)

Table 1 shows the quadratic rate of convergence, defined using a relation similar to equation (8) for the coefficients of the two factors, A and B.

 

iter A B

1 0.0364715122 0.0442032255

2 0.0029259326 0.0002011458

3 0.0000014305 0.0000000199

4 0.0000000894 0.0000000199

5 0.0000000596 0.0000000000

6 0.0000000000 0.0000000000