Forward Interpolation

Forward interpolation plays only a supplementary role in this paper, but it has many applications of its own in the seismic processing practice. It is sufficient to mention such applications as trace resampling, NMO, Kirchoff and Stolt migrations, log-stretch, radial transform, etc. Two simple examples appear at the end of this section.

The general form of a linear forward interpolation operator is  

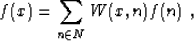$$f (x) = \sum_{n \in N} W (x, n) f (n)\;,$$ (1)

where n is a point on a given regular grid N, x is a point in the continuum, f(x) is the reconstructed continuous function, and W(x,n) is a linear weight. Although in the discussion that follows, I refer to only the one-dimensional theory, a generalization to many dimensions is straightforward.