




Next: Antialiasing
Up: Biondi, Fomel & Chemingui:
Previous: REFERENCES
In this Appendix, we describe the main characteristics
of our implementation of the Kirchhoff AMO operator.
This implementation is based on analysis
presented in previous reports
Biondi and Chemingui (1994); Chemingui and Biondi (1995); Fomel and Biondi (1995a,b).
The AMO integration surface has the shape of a saddle.
The exact shape of the saddle depends on the
azimuth rotation and offset continuation
that are applied to the input data.
When the azimuth rotation is small,
the saddle has a strong curvature that makes
its straightforward integral
implementation inaccurate.
We address this problem by performing
the spatial integration
in a transformed coordinate system.
In this new coordinate system, the AMO surface is
well behaved, and its shape is
invariant with respect to the amount of azimuth rotation
and offset continuation.
The appropriate coordinate transformation is described by
the following chain of transformations
| ![\begin{displaymath}
\left[
\begin{array}
{c}
z_1 \
z_2 \
\end{array} \...
...\left[
\begin{array}
{c}
x_m \
y_m \end{array} \right]\;,\end{displaymath}](img1.gif) |
(1) |
where xm and ym are the original midpoint coordinates,
z1, and z2 are the transformed coordinates,
and 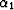 and
and 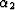 are respectively
the azimuth of the input trace and the azimuth of the output trace.
The right matrix represents a space invariant rotational
squeezing of the coordinate, while the left matrix
is a simple rescaling of the axes by a factor dependent
on the azimuth rotation
are respectively
the azimuth of the input trace and the azimuth of the output trace.
The right matrix represents a space invariant rotational
squeezing of the coordinate, while the left matrix
is a simple rescaling of the axes by a factor dependent
on the azimuth rotation 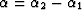 .When the azimuth rotation is zero, the transformation
described in equation (1)
becomes singular.
In this case the AMO operator degenerates into
the 2-D offset continuation
operator Biondi and Chemingui (1994); Fomel (1995).
In practice,
a simple pragmatic method to avoid the singularity
is to set a lower limit for the product
.When the azimuth rotation is zero, the transformation
described in equation (1)
becomes singular.
In this case the AMO operator degenerates into
the 2-D offset continuation
operator Biondi and Chemingui (1994); Fomel (1995).
In practice,
a simple pragmatic method to avoid the singularity
is to set a lower limit for the product
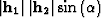 .Since the 3-D AMO operator converges smoothly to the
2-D offset continuation operator Fomel and Biondi (1995a),
the error introduced by this approximation
is negligible.
In this new coordinate system, the kinematics
of AMO are described by the following simple
relationship between the input time t1 and the
output time t2.
.Since the 3-D AMO operator converges smoothly to the
2-D offset continuation operator Fomel and Biondi (1995a),
the error introduced by this approximation
is negligible.
In this new coordinate system, the kinematics
of AMO are described by the following simple
relationship between the input time t1 and the
output time t2.
| 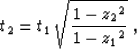 |
(2) |
and the amplitudes (based on Zhang-Black amplitudes for DMO)
are described by the following equation
| 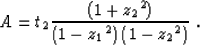 |
(3) |
Notice that this expression for the amplitudes does already take into
account the Jacobian of the transformation
described in (equation (1)).
The result of the AMO integral needs also to be
half-differentiated twice, once with a causal and once
with an anti-causal differentiator.





Next: Antialiasing
Up: Biondi, Fomel & Chemingui:
Previous: REFERENCES
Stanford Exploration Project
6/14/2000
![\begin{displaymath}
\left[
\begin{array}
{c}
z_1 \
z_2 \
\end{array} \...
...\left[
\begin{array}
{c}
x_m \
y_m \end{array} \right]\;,\end{displaymath}](img1.gif)
![\begin{displaymath}
\left[
\begin{array}
{c}
z_1 \
z_2 \
\end{array} \...
...\left[
\begin{array}
{c}
x_m \
y_m \end{array} \right]\;,\end{displaymath}](img1.gif)