Next: Operator aperture
Up: IMPLEMENTATION OF INTEGRAL AMO
Previous: IMPLEMENTATION OF INTEGRAL AMO
The AMO operator can be steeply dipping,
and thus it is crucial to apply
antialiasing to produce high-quality results.
We apply antialiasing by a simple low-pass filtering
of the input trace. The bandwidth of this low-pass filtering
varies spatially along the operator and is a function
of the local time dips of the operator.
The time dips can be computed
analytically according to the following equations:
| 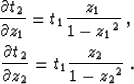 |
(4) |
| (5) |





Next: Operator aperture
Up: IMPLEMENTATION OF INTEGRAL AMO
Previous: IMPLEMENTATION OF INTEGRAL AMO
Stanford Exploration Project
6/14/2000