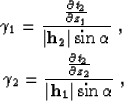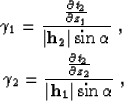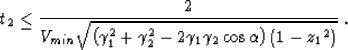Operator aperture

The expression for the kinematic and amplitudes of AMO [equations ((2) and (3))] are valid for z₁ and z₂ ranging between -1 and 1. However, for finite propagation velocities, the AMO operator has much narrower aperture. Taking into account this finite aperture is crucial both for accuracy and for efficiency. For a given minimum propagation velocity V_min, the maximum output time can be evaluated according to the following expressions, as derived in Fomel and Biondi (1995a):

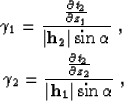$$\begin{eqnarray} \gamma_1=\frac{\frac{\partial t_2}{\partial z_1}}{\left\vert{\b... ...l t_2}{\partial z_2}}{\left\vert{\bf h_1}\right\vert\sin\alpha}\;,\end{eqnarray}$$ (6) (7)

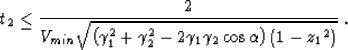$$t_2 \leq \frac{2}{V_{min}\sqrt{\left(\gamma_1^2 + \gamma_2^2 -2 \gamma_1\gamma_2\cos\alpha\right)\left(1-{z_1}^2\right)}}\;.$$ (8)

To avoid truncation artifacts, we use a tapering function at the edges of the operator aperture.