Resolution and random signals

  The accuracy of measurements on observed signals is limited not only by practical realities, but also by certain fundamental principles. The most famous example included in this chapter is the time-bandwidth product in Fourier-transformation theory, called the ``uncertainty principle.''

Observed signals often look random and are often modeled by filtered random numbers. In this chapter we will see many examples of signals built from random numbers and discover how the nomenclature of statistics applies to them. Fundamentally, this chapter characterizes ``resolution,'' resolution of frequency and arrival time, and the statistical resolution of signal amplitude and power as functions of time and frequency.

We will see $\sqrt{n}$ popping up everywhere. This $\sqrt{n}$ enters our discussion when we look at spectra of signals built from random numbers. Also, signals that are theoretically uncorrelated generally appear to be weakly correlated at a level of $1/\sqrt{n}$, where n is the number of independent points in the signal.

Measures of resolution (which are variously called variances, tolerances, uncertainties, bandwidths, durations, spreads, rise times, spans, etc.) often interact with one another, so that experimental change to reduce one must necessarily increase another or some combination of the others. In this chapter we examine basic cases where such conflicting interactions occur.

To avoid confusion I introduce the unusual notation $\Lambda$where $\Delta$ is commonly used. Notice that the letter $\Lambda$ resembles the letter $\Delta$,and $\Lambda$ connotes length without being confused with wavelength. Lengths on the time and frequency axes are defined as follows:

		dt, df 		mesh intervals in time and frequency
		$\Delta t$, $\Delta f$ 		mesh intervals in time and frequency
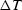
		$\Delta T$ $\Delta F$ 		extent of time and frequency axis
		$\Lambda T$, $\Lambda F$ time duration and     spectral bandwidth of a signal

There is no mathematically tractable and universally acceptable definition for time span $\Lambda T$and spectral bandwidth $\Lambda F$.A variety of defining equations are easy to write, and many are in general use. The main idea is that the time span $\Lambda T$ or the frequency span $\Lambda F$should be able to include most of the energy but need not contain it all. The time duration of a damped exponential function is infinite if by duration we mean the span of nonzero function values. However, for practical purposes the time span is generally defined as the time required for the amplitude to decay to e^-1 of its original value. For many functions the span is defined by the span between points on the time or frequency axis where the curve (or its envelope) drops to half of the maximum value. Strange as it may sound, there are certain concepts about the behavior of $\Lambda T$ and $\Lambda F$that seem appropriate for ``all'' mathematical choices of their definitions, yet these concepts can be proven only for special choices.