




Next: FT OF RANDOM NUMBERS
Up: My rise-time form of
Previous: My rise-time form of
We omit the details
of the proof of the rise time form of the uncertainty principle
which are found in PVI
and mention instead a few insights found along with the proof.
The ``slack'' in the uncertainty principle relates
to comparing the duration of a signal 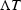 to the
duration of its autocorrelation
to the
duration of its autocorrelation 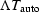 .Generally speaking,
it is easy to find a long signal that has short autocorrelation.
Just take an arbitrary short signal
and convolve it using a lengthy all-pass filter.
Conversely, we cannot get a long autocorrelation function
from a short signal.
A good example is the autocorrelation of a rectangle function,
which is a triangle.
The triangle appears to be twice as long,
but considering that the triangle tapers down,
it is reasonable to assert that the
.Generally speaking,
it is easy to find a long signal that has short autocorrelation.
Just take an arbitrary short signal
and convolve it using a lengthy all-pass filter.
Conversely, we cannot get a long autocorrelation function
from a short signal.
A good example is the autocorrelation of a rectangle function,
which is a triangle.
The triangle appears to be twice as long,
but considering that the triangle tapers down,
it is reasonable to assert that the 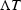 's are the same.
Thus, we conclude that
's are the same.
Thus, we conclude that
| 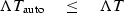 |
(4) |
From this inequality may be proven the inequality
in the uncertainty relation
| 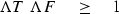 |
(5) |





Next: FT OF RANDOM NUMBERS
Up: My rise-time form of
Previous: My rise-time form of
Stanford Exploration Project
3/1/2001