A similar and possibly more basic concept
than the product of time and frequency spreads
is the relationship between spectral bandwidth
and the ``rise time'' of a system-response function.
The rise time ![]() of a system response is defined
as follows:
when we kick a physical system with an impulse function,
it usually responds rapidly,
rising to some maximum level,
and then dropping off more slowly toward zero.
The quantitative value of the rise time is generally, and
somewhat arbitrarily,
taken to be the span between
the time of excitation and the time at which the system
response is more than halfway up to its maximum.
of a system response is defined
as follows:
when we kick a physical system with an impulse function,
it usually responds rapidly,
rising to some maximum level,
and then dropping off more slowly toward zero.
The quantitative value of the rise time is generally, and
somewhat arbitrarily,
taken to be the span between
the time of excitation and the time at which the system
response is more than halfway up to its maximum.
``Tightness" (nearness to equality) in the inequality (1) is associated with minimum phase. ``Slackness" (remoteness from equality) in the (1) would occur if a filter with an additional all-pass component were used. Slackness could also be caused by a decay time that is more rapid than the rise time, or by other combinations of rises and falls, such as random combinations. Physical systems generally respond rapidly compared to the rate at which they later decay. Focusing our attention on such systems, we can now seek to derive the inequality (1) applied to rise time and bandwidth.
The first step is to choose a definition for rise time. I have found a tractable definition of rise time to be
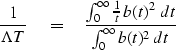 |
(3) |