




Next: Coherency
Up: CROSSCORRELATION AND COHERENCY
Previous: CROSSCORRELATION AND COHERENCY
``Correlation"
is a concept similar to cosine.
A cosine measures the angle between two vectors.
It is given by the dot product of the two vectors
divided by their magnitudes:
| 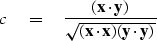 |
(31) |
This is the
sample normalized correlation.
Formally, the
normalized correlation
is defined using
x and y as zero-mean, scalar, random variables
instead of sample vectors.
The summation is thus an expectation instead of a dot product:
| 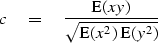 |
(32) |
A practical difficulty arises
when the ensemble averaging is simulated over a sample.
The problem occurs with small samples
and is most dramatically illustrated when we deal with
a sample of only one element.
Then the sample correlation is
| 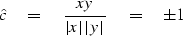 |
(33) |
regardless of what value the random number x
or the random number y should take.
For any n, the sample correlation 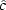 scatters away from zero.
Such scatter is called ``bias."
The topic of bias and variance of coherency estimates is a complicated one,
but a rule of thumb seems to be to expect bias and variance
of
scatters away from zero.
Such scatter is called ``bias."
The topic of bias and variance of coherency estimates is a complicated one,
but a rule of thumb seems to be to expect bias and variance
of 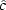 of about
of about 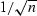 for samples of size n.
Bias, no doubt, accounts for many false ``discoveries,''
since cause-and-effect is often inferred from correlation.
for samples of size n.
Bias, no doubt, accounts for many false ``discoveries,''
since cause-and-effect is often inferred from correlation.





Next: Coherency
Up: CROSSCORRELATION AND COHERENCY
Previous: CROSSCORRELATION AND COHERENCY
Stanford Exploration Project
3/1/2001