Differentiator

Calculus defines the differential of a time function like this

$${d\ \over dt}\ f(t) \eq \lim_{\Delta t \rightarrow 0} { f(t) \ - \ f(t-\Delta t) \over \Delta t}$$

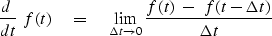
Computationally, we think of a differential as a finite difference, namely, a function is delayed a bit and then subtracted from its original self. Expressed as a Z-transform, the finite difference operator is (1-Z) with an implicit 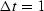$\Delta t=1$.In the language of filters, the time derivative is the filter (+1,-1).

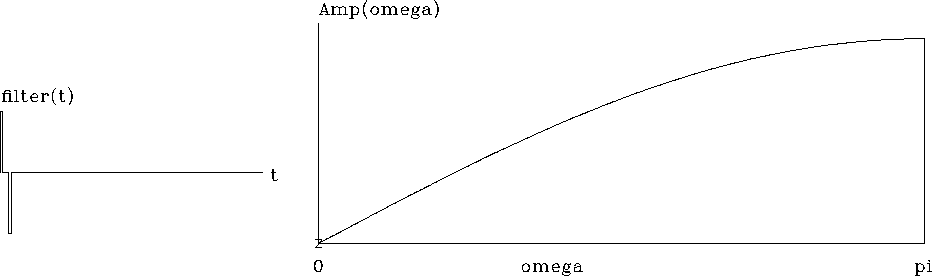
The filter (1-Z) is often simply called a ``differentiator.'' It is displayed in Figure 6. Notice its amplitude spectrum increases with frequency.

 

ddt
Figure 6 A discrete representation of the first-derivative operator. The filter (1,-1) is plotted on the left, and on the right is an amplitude response, i.e., |1-Z| versus $\omega$.

Theoretically, the amplitude spectrum of a time derivative operator increases linearly with frequency. Here is why. Begin from Fourier representation of a time function (15).

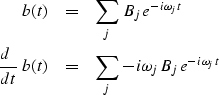$$\begin{eqnarray} b(t) &=& \sum_j \, B_j \, e^{-i\omega_j t} \\ {d\ \over dt}\ b(t) &=& \sum_j \, -i \omega_j B_j \, e^{-i\omega_j t}\end{eqnarray}$$ (22) (23)

and notice that where the original function has Fourier coefficients B_j, the time derivative has Fourier coefficients 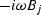$-i\omega B_j$.

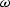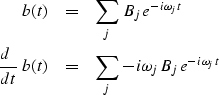
In Figure 6 we notice the spectrum begins looking like a linear function of $\omega$,but at higher frequencies, it curves. This is because at high frequencies, a finite difference is different from a differential.