Next: Sampled time and Nyquist
Up: FOURIER SUMS
Previous: FOURIER SUMS
Fourier analysis is built from the complex exponential
| 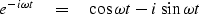 |
(13) |
A Fourier component of a time signal is a complex number,
a sum of real and imaginary parts,
say
| 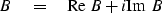 |
(14) |
which is attached to some frequency.
Let j be an integer
and 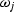 be a set of frequencies.
A signal b(t) can be manufactured
by adding a collection of complex exponential signals,
each complex exponential being scaled by a complex coefficient Bj,
namely,
be a set of frequencies.
A signal b(t) can be manufactured
by adding a collection of complex exponential signals,
each complex exponential being scaled by a complex coefficient Bj,
namely,
| 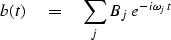 |
(15) |
This manufactures a complex-valued signal.
How do we arrange for b(t) to be real?
We can throw away the imaginary part, which is like
adding b(t) to its complex conjugate 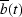 ,and then dividing by two:
,and then dividing by two:
| 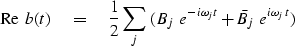 |
(16) |
In other words, for each positive 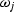 with amplitude Bj,
we add a negative
with amplitude Bj,
we add a negative 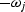 with amplitude
with amplitude 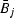 (likewise, for every negative
(likewise, for every negative 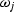 ...).
The Bj are called the
``frequency function,''
or the ``Fourier transform.''
Loosely, the Bj are called the ``spectrum,'' though
in formal mathematics,
the word
``spectrum'' is reserved for the product
...).
The Bj are called the
``frequency function,''
or the ``Fourier transform.''
Loosely, the Bj are called the ``spectrum,'' though
in formal mathematics,
the word
``spectrum'' is reserved for the product
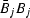 .The words ``amplitude spectrum'' universally mean
.The words ``amplitude spectrum'' universally mean
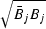 .
.
In practice, the collection of frequencies is almost always evenly spaced.
Let j be an integer 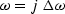 so that
so that
| 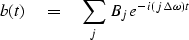 |
(17) |
Representing a signal by a sum of sinusoids
is technically known as
``inverse Fourier transformation.''
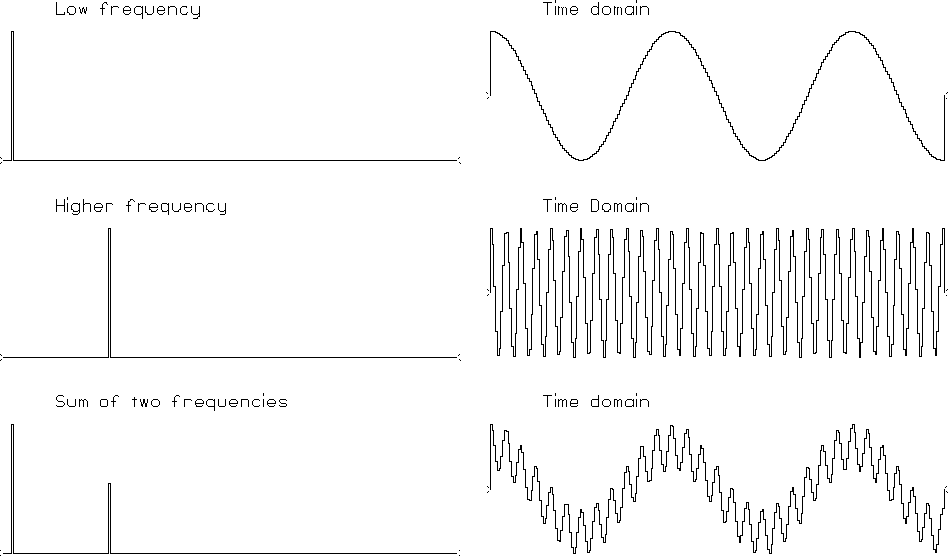
An example of this is shown in Figure 5.
cosines
Figure 5
Superposition of two sinusoids.






Next: Sampled time and Nyquist
Up: FOURIER SUMS
Previous: FOURIER SUMS
Stanford Exploration Project
3/1/2001
![]() .
.![]() so that
so that