




Next: Digression: curl grad as
Up: Model fitting by least
Previous: INVERSE NMO STACK
Vesuvius
phase unwrapping
phase
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
radar
shows
radar![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) images of
Mt. Vesuvius
images of
Mt. Vesuvius![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) in Italy.
These images are made from backscatter
signals s1(t) and s2(t),
recorded along two satellite orbits 800 km high and 54 m apart.
The signals are very high frequency
(the radar wavelength being 2.7 cm).
They were Fourier transformed
and one multiplied by the complex conjugate of the other,
getting the product
in Italy.
These images are made from backscatter
signals s1(t) and s2(t),
recorded along two satellite orbits 800 km high and 54 m apart.
The signals are very high frequency
(the radar wavelength being 2.7 cm).
They were Fourier transformed
and one multiplied by the complex conjugate of the other,
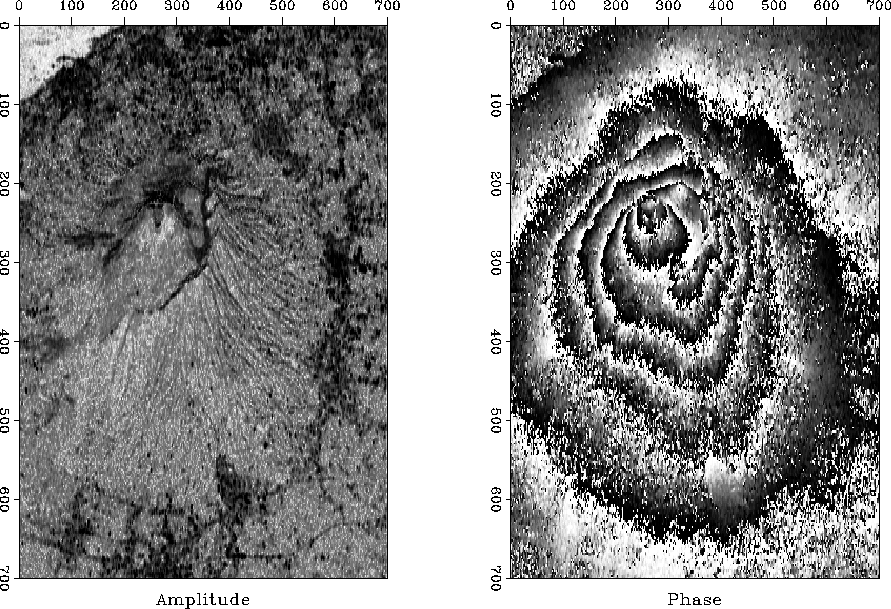
getting the product 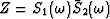 .The product's amplitude and phase are shown in Figure
.The product's amplitude and phase are shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Examining the data,
you can notice that where the signals are strongest (darkest on the left),
the phase (on the right)
is the most spatially consistent.
Pixel by pixel evaluation with the two frames in a movie program
shows that there are a few somewhat large local amplitudes
(clipped in Figure
.
Examining the data,
you can notice that where the signals are strongest (darkest on the left),
the phase (on the right)
is the most spatially consistent.
Pixel by pixel evaluation with the two frames in a movie program
shows that there are a few somewhat large local amplitudes
(clipped in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
but because these generally have spatially consistent phase,
I would not describe the data as containing noise bursts.
vesuvio90
)
but because these generally have spatially consistent phase,
I would not describe the data as containing noise bursts.
vesuvio90
Figure 2
Radar image of Mt. Vesuvius.
Left is the amplitude.
Non-reflecting ocean in upper left corner.
Right is the phase.
(Umberto Spagnolini)
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





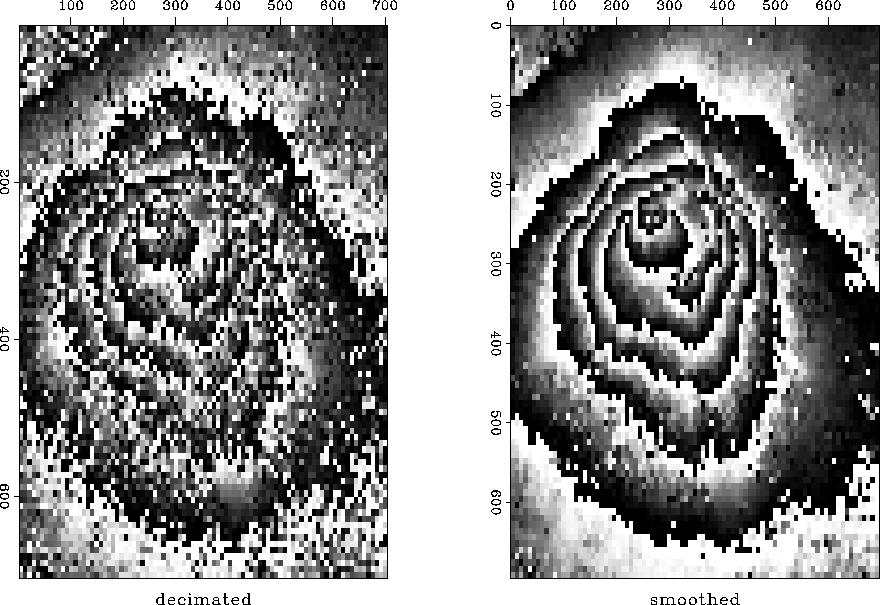
To reduce the time needed for analysis and printing,
I reduced the data size two different ways,
by decimation and by local averaging,
as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The decimation was to about 1 part in 9 on each axis,
and the local averaging was done in
.
The decimation was to about 1 part in 9 on each axis,
and the local averaging was done in 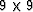 windows
giving the same spatial resolution in each case.
The local averaging was done independently in the
plane of the real part and the plane of the imaginary part.
Putting them back together again showed that the phase
angle of the averaged data behaves much more consistently.
This adds evidence that the data is not troubled by noise bursts.
windows
giving the same spatial resolution in each case.
The local averaging was done independently in the
plane of the real part and the plane of the imaginary part.
Putting them back together again showed that the phase
angle of the averaged data behaves much more consistently.
This adds evidence that the data is not troubled by noise bursts.
squeeze90
Figure 3
Phase based on decimated data (left)
and smoothed data (right).
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





From Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we see that contours of constant phase
appear to be contours of constant altitude;
this conclusion leads us to suppose that a study of radar theory
would lead us to a relation like Z=eih
where h is altitude (in units unknown to us nonspecialists).
Because the flat land away from the mountain is all at the same phase
(as is the altitude),
the distance as revealed by the phase does not represent
the distance from the ground to the satellite viewer.
We are accustomed to measuring altitude along a vertical line to a datum,
but here the distance seems to be measured
from the ground along a
we see that contours of constant phase
appear to be contours of constant altitude;
this conclusion leads us to suppose that a study of radar theory
would lead us to a relation like Z=eih
where h is altitude (in units unknown to us nonspecialists).
Because the flat land away from the mountain is all at the same phase
(as is the altitude),
the distance as revealed by the phase does not represent
the distance from the ground to the satellite viewer.
We are accustomed to measuring altitude along a vertical line to a datum,
but here the distance seems to be measured
from the ground along a 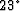 angle from the vertical
to a datum at the satellite height.
angle from the vertical
to a datum at the satellite height.
Phase is a troublesome measurement because
we generally see it modulo 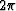 .Marching up the mountain we see the phase getting lighter and lighter
until it suddenly jumps to black which then continues to lighten
as we continue up the mountain to the next jump.
Let us undertake to compute the phase including
all of its jumps of
.Marching up the mountain we see the phase getting lighter and lighter
until it suddenly jumps to black which then continues to lighten
as we continue up the mountain to the next jump.
Let us undertake to compute the phase including
all of its jumps of 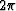 .Begin with a complex number Z representing
the complex-valued image at any location
in the (x,y)-plane.
.Begin with a complex number Z representing
the complex-valued image at any location
in the (x,y)-plane.
| 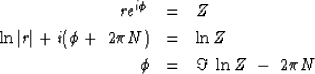 |
(68) |
| (69) |
| (70) |
A computer will find the imaginary part of the logarithm
with the arctan function of two arguments, atan2(y,x),
which will put the phase in the range 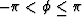 although any multiple of
although any multiple of 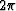 could be added.
We seem to escape the
could be added.
We seem to escape the 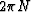 phase ambiguity by differentiating:
phase ambiguity by differentiating:
| 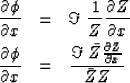 |
(71) |
| (72) |
For every point on the y-axis, equation (72)
is a differential equation on the x-axis,
and we could integrate them all to find 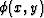 .That sounds easy.
On the other hand,
the same equations are valid when x and y are interchanged,
so we get twice as many equations as unknowns.
For ideal data, either of these sets of equations
should be equivalent to the other,
but for real data we expect to be fitting the fitting goal
.That sounds easy.
On the other hand,
the same equations are valid when x and y are interchanged,
so we get twice as many equations as unknowns.
For ideal data, either of these sets of equations
should be equivalent to the other,
but for real data we expect to be fitting the fitting goal
| 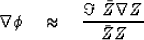 |
(73) |
where
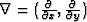 .
.
We will be handling the differential equation as a difference equation
using an exact representation on the data mesh.
By working with the phase difference of neighboring data values,
we do not have to worry about phases greater than 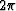 (except where phase jumps that much between mesh points).
Thus we solve (73)
with finite differences instead of differentials.
Module igrad2 is a linear operator for the difference
representation of the operator representing
the gradient of a potential field.
Its adjoint is known as the divergence of a vector field.
igrad2gradient in 2-D
To do the least-squares fitting
(73)
we pass the igrad2 module to the Krylov subspace solver.
(Other people might prepare a matrix and give it to Matlab.)
(except where phase jumps that much between mesh points).
Thus we solve (73)
with finite differences instead of differentials.
Module igrad2 is a linear operator for the difference
representation of the operator representing
the gradient of a potential field.
Its adjoint is known as the divergence of a vector field.
igrad2gradient in 2-D
To do the least-squares fitting
(73)
we pass the igrad2 module to the Krylov subspace solver.
(Other people might prepare a matrix and give it to Matlab.)
The difference equation representation of the fitting goal
(73) is:
| 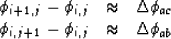 |
(74) |
where we still need to define the right-hand side.
Define the parameters
a,
b,
c, and
d as follows:
| ![\begin{displaymath}
\left[
\begin{array}
{ll}
a & b \\ c & d
\end{array} \ri...
...j} & Z_{i,j+1} \\ Z_{i+1,j} & Z_{i+1,j+1}
\end{array} \right]\end{displaymath}](img182.gif) |
(75) |
Arbitrary complex numbers a and b may be expressed in polar form,
say 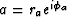 and
and 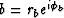 .The complex number
.The complex number
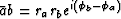 has the desired phase
has the desired phase
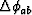 .To obtain it we take the imaginary part of the complex logarithm
.To obtain it we take the imaginary part of the complex logarithm
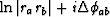 .
.
| 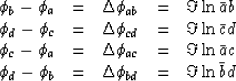 |
(76) |
which gives the information needed to fill in the right-hand side of
(74), as done by subroutine igrad2init() from
module unwrap ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
radar
shows
radar![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) images of
Mt. Vesuvius
images of
Mt. Vesuvius![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) in Italy.
These images are made from backscatter
signals s1(t) and s2(t),
recorded along two satellite orbits 800 km high and 54 m apart.
The signals are very high frequency
(the radar wavelength being 2.7 cm).
They were Fourier transformed
and one multiplied by the complex conjugate of the other,
getting the product
in Italy.
These images are made from backscatter
signals s1(t) and s2(t),
recorded along two satellite orbits 800 km high and 54 m apart.
The signals are very high frequency
(the radar wavelength being 2.7 cm).
They were Fourier transformed
and one multiplied by the complex conjugate of the other,
getting the product ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Examining the data,
you can notice that where the signals are strongest (darkest on the left),
the phase (on the right)
is the most spatially consistent.
Pixel by pixel evaluation with the two frames in a movie program
shows that there are a few somewhat large local amplitudes
(clipped in Figure
.
Examining the data,
you can notice that where the signals are strongest (darkest on the left),
the phase (on the right)
is the most spatially consistent.
Pixel by pixel evaluation with the two frames in a movie program
shows that there are a few somewhat large local amplitudes
(clipped in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
but because these generally have spatially consistent phase,
I would not describe the data as containing noise bursts.
)
but because these generally have spatially consistent phase,
I would not describe the data as containing noise bursts.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The decimation was to about 1 part in 9 on each axis,
and the local averaging was done in
.
The decimation was to about 1 part in 9 on each axis,
and the local averaging was done in ![]() windows
giving the same spatial resolution in each case.
The local averaging was done independently in the
plane of the real part and the plane of the imaginary part.
Putting them back together again showed that the phase
angle of the averaged data behaves much more consistently.
This adds evidence that the data is not troubled by noise bursts.
windows
giving the same spatial resolution in each case.
The local averaging was done independently in the
plane of the real part and the plane of the imaginary part.
Putting them back together again showed that the phase
angle of the averaged data behaves much more consistently.
This adds evidence that the data is not troubled by noise bursts.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we see that contours of constant phase
appear to be contours of constant altitude;
this conclusion leads us to suppose that a study of radar theory
would lead us to a relation like Z=eih
where h is altitude (in units unknown to us nonspecialists).
Because the flat land away from the mountain is all at the same phase
(as is the altitude),
the distance as revealed by the phase does not represent
the distance from the ground to the satellite viewer.
We are accustomed to measuring altitude along a vertical line to a datum,
but here the distance seems to be measured
from the ground along a
we see that contours of constant phase
appear to be contours of constant altitude;
this conclusion leads us to suppose that a study of radar theory
would lead us to a relation like Z=eih
where h is altitude (in units unknown to us nonspecialists).
Because the flat land away from the mountain is all at the same phase
(as is the altitude),
the distance as revealed by the phase does not represent
the distance from the ground to the satellite viewer.
We are accustomed to measuring altitude along a vertical line to a datum,
but here the distance seems to be measured
from the ground along a ![]() angle from the vertical
to a datum at the satellite height.
angle from the vertical
to a datum at the satellite height.
![]() .Marching up the mountain we see the phase getting lighter and lighter
until it suddenly jumps to black which then continues to lighten
as we continue up the mountain to the next jump.
Let us undertake to compute the phase including
all of its jumps of
.Marching up the mountain we see the phase getting lighter and lighter
until it suddenly jumps to black which then continues to lighten
as we continue up the mountain to the next jump.
Let us undertake to compute the phase including
all of its jumps of ![]() .Begin with a complex number Z representing
the complex-valued image at any location
in the (x,y)-plane.
.Begin with a complex number Z representing
the complex-valued image at any location
in the (x,y)-plane.
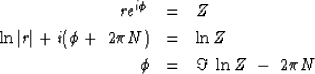
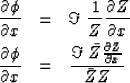
![]() (except where phase jumps that much between mesh points).
Thus we solve (73)
with finite differences instead of differentials.
Module igrad2 is a linear operator for the difference
representation of the operator representing
the gradient of a potential field.
Its adjoint is known as the divergence of a vector field.
igrad2gradient in 2-D
To do the least-squares fitting
(73)
we pass the igrad2 module to the Krylov subspace solver.
(Other people might prepare a matrix and give it to Matlab.)
(except where phase jumps that much between mesh points).
Thus we solve (73)
with finite differences instead of differentials.
Module igrad2 is a linear operator for the difference
representation of the operator representing
the gradient of a potential field.
Its adjoint is known as the divergence of a vector field.
igrad2gradient in 2-D
To do the least-squares fitting
(73)
we pass the igrad2 module to the Krylov subspace solver.
(Other people might prepare a matrix and give it to Matlab.)
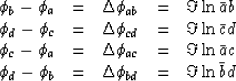
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.